THE PHYSICS AND PATHOLOGY OF WOUNDS

PART 3: CHRONICITY AND THE PHYSICS OF WOUND FAILURE

Marc E. Gottlieb, MD, FACS

Phoenix, AZ

Revision 01-c, June 2, 2010, (Revision 01-a, February 10, 2010), Copyright © 2010

Preamble

In Part 1 of this series, The Wound as a System and a Controlled Machine, the main point was that the wound is not only a complex system, but it is a non-linear controlled system. Control is the basis for all wound dynamics, allowing the healthy wound to heal by one-shot dynamics, but leading to complex patterns when wound healing is pathological. In Part 2, Auto-Immunopathy and the Intrinsic Disease of Wound Healing, we went from a physics-engineering perspective to a clinical-pathological one. The general stroma, the auto-immune connective tissue disorders, and the chronic wound were all equated through the principle of sustained chronic inflammation leading to immune sensitization against stromal elements. Now, in Part 3, Chronicity and the Intrinsic Disease of Wound Healing, we will bring together the engineering aspects of the wound as a controlled process and the clinico-pathological aspects of intrinsic auto-immune wound chronicity to understand why chronic wounds fail to heal. This is a physics based understanding that uses the principles of non-linear dynamics (the physics of systems) to explain why the wound control loop cannot succeed in the face of stromal auto-immunization and intrinsic wound chronicity.

1

In Part 1 of this series, we looked at the wound as a system subject to feedback and control. This model of the wound can accommodate all conditions of wound physiology and pathology, of normality, failure, and therapy. In Part 2, intrinsic wound pathology and failure were examined, the condition of intrinsic degradation of wound healing not attributable to extrinsic factors. This intrinsic disease of wound healing results from the appearance of an abnormal population of chronic inflammatory and immune cells which has complex disruptive effects on the two cell sets which belong there, acute inflammation and wound module. These states have a critical association with autoimmunity, microthrombosis, and other events which sustain inflammation. From a biological perspective, it is easy enough to see how the chronic inflammation might disrupt healing. However, isn’t the purpose of the Wound Control Loop to respond to and correct perturbation? There are reasons why the chronic wound cannot respond as expected, and this is where the engineering science of Part 1 and the biosciences of Part 2 meet to explain the physics of wound failure and wound chronicity.

2

The wound is not just a tissue. It has multiple substructures, a complex organization, and complex tasks. It is not a constituent tissue of some other organ. It is itself an organ. The wound is an organ. When we say “wound” here, we are not talking about the injury nor the physical defect caused by the injury, but rather about the wound repair process, the “wound module”, which is the body’s response to the injury and defect. It is a reserve anatomy and physiology, a transient ad hoc organ that is triggered into existence by injury, then performs its appointed functions, then wanes and disappears as its job is completed. Nonetheless, it has the structure and functions that conceptualize any other fixed organ. So, we will start by comparing wound healing to other organs. For any organ, ask 3 questions:

What are its quintessential structures and functions?

What is the quintessence of its dysfunction or failure?

What is the fundamental physics relevant to its function?

The heart is a complex organ, with great complexity to its structure and function. However, its quintessence is that it is a pump with valves and pipes. When it fails, it is an inadequate pump, damming the circulation. Some knowledge of fluid mechanics is required to understand its basic physiology and pathology. The quintessence of the kidney is that it is a filter and resorption membrane. When it fails, it is tantamount to an occluded filter in any fluid system. Basic hydraulics and ionic chemistry are the core physical sciences that apply. The lung is essentially just a bellows and diffusion membrane, and when faulty, ventilation and respiration are impaired. Gas mechanics and diffusion are the applicable physics. The eye is a light collector and detector, its failure is blindness, and optics apply. The ear is a sound transducer and decoder, its failure is deafness, and acoustics apply. Skeletal structures are structural members, their failure impairs support and mobility, and solid mechanics apply. Nerves are electrical control circuits, their failure is equivalent to open circuits and faulty electrical transmission, and electricity is the relevant physics.

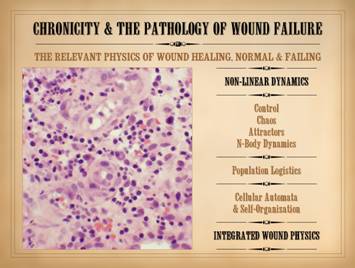
What then is the quintessential structure and function of the wound? What is the quintessential derangement of intrinsic wound pathology and chronicity? What are the fundamental or constitutive physical sciences – the physics – relevant to the wound?

3

What then is the quintessential structure and function of the wound? It is just a bunch of cells that get together, make some stuff, then quiet down or disappear. What stuff are they making? They are making stroma. They are making, repairing, or restoring the basic structural medium of the body, a composite material made of ground substance, connective proteins, and blood vessels. They are making or restoring the basic framing and utilities that the body needs to support all of the other parenchymal cells and structures that have a more specific or parochially defined role. Correctly stated, the quintessence of wound anatomy (i.e. wound repair / wound module) is a collection of mutually interactive self-organizing cell populations.

What is the quintessential derangement of intrinsic wound pathology and chronicity? It is what happens when this collection of self-organizing cells fails to organize to make new stroma. It is what happens when they fail to make new stroma due to their own disorganization and failed inter-operations, rather than due to any extrinsically applied perturbation. New stroma depends on these cells getting together into the right pattern and structure. If they fail to organize then the new stroma is incorrect and cannot support associated parenchyma (like the epithelium, and thus the wound does not close). In the words of its relevant physics, the quintessential derangement or failure of this self-organizing system is that it is a dynamical disorder of logistical self-re-organization among these populations.

What are the fundamental or constitutive physical sciences – the physics – relevant to the wound? The concepts of self-organization, population dynamics, and mutual interaction are part of the subject of non-linear dynamics, including control, chaos, population logistics, and cellular automata. For other organs, the relevant physics are mechanics, fluids, gases, optics, acoustics, electricity, etc. For the wound, it is non-linear dynamics.

4

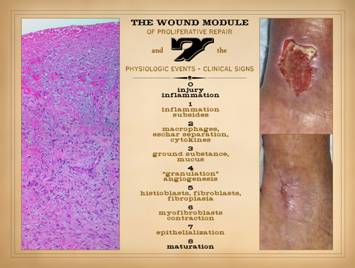
This slide comes from Part 1 of this series, “The Wound as a System and a Controlled Machine”, slide 7. It is meant to refresh a few points about basic wound anatomy and physiology. On this slide, on the right, a normal healthy wound goes from open to closed (contracted and epithelialized) via the natural process of wound healing. Histologically, all of the reparative events taking place in the wound have a well organized and recognizable anatomy, and each of the features seen microscopically correlates with something that is happening or can be observed grossly. Major events and correlated physical findings are:

0 – Injury and inflammation: They trigger the whole process of response and repair. The repair process is a reserve organ that arises only as needed.

1 – Inflammation subsides: Acute inflammation is the response to injury that includes initiating repair. However, sustained acute inflammation is suppressive to wound repair. For incidental injury, inflammation is a one-shot response that wanes as repair rises. As will be presented here, sustained primary injury and sustained acute inflammation are one of the essential dynamics required for wound chronicity.

2 – Macrophages, eschar separation, and cytokines: Macrophages are transformed leukocytes, arrived by inflammation, that have two major roles. Their afferent task is as phagocytic cells to remove debris. This becomes relevant to chronic wound pathology since this activity is a key step in stromal auto-immunization. Their efferent task is to initiate the repair process by the issue of proliferative growth factors.

3 – Ground substance and mucus: In advance of a formal fibrous stroma or structure in the wound, aminoglycan ground substance is the medium which early angioid cells need in order to migrate and function.

4 – “Granulation tissue” and angiogenesis: Proliferative angiogenesis creates the vascular network required for subsequent cells and activities to function. Once this occurs, fibroplasia and restoration of structural stroma can proceed.

5 – Fibroblasts, and fibroplasia: Once angiocytes have formed vessels within the aminoglycan layer, the environment now permits fibroblasts to function. Fibroblasts make the connective proteins required for a mechanically durable stroma.

6 – Myofibroblasts and contraction: To get the wound closed, specialized fibroblasts with muscle proteins contract the wound, minimizing its surface area, lightening the load on epithelialization.

7 – Epithelialization: Final closure of the wound is when epithelium is fully resurfaced, sequestering the mesenchymal stroma underneath from the ambient environment.

8 – Maturation: Maturation is a long process in which the excessive stroma of the newly healed wound remodels back to vascular and connective protein densities and architecture which match normal dermis and fascias.

The vertical anatomy of the wound reflects timewise events and sequences. The surface is happening now. The fibroplasia layer deeper down started so many days ago. Separation of cells and populations (acute inflammation and wound module) by time and strata are a crucial part of this physiology. They become intermixed in the pathological wound.

5

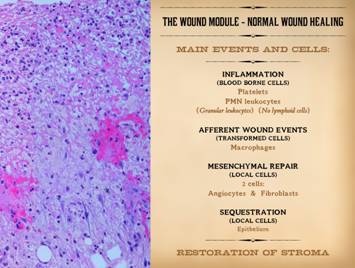
This slide also comes from Part 1 of this series. It is meant to remind that normal wound healing has some general phases. The response to acute injury is thrombosis and acute inflammation, dependent on blood borne leukocytes. This transitions into afferent wound events, mediated by transformed leukocytes, which includes triggering the efferent reparative wound events. Repair is mediated by mesenchymal cells with two – and only two – phenotypes, the angiocyte and the fibroblast. Wound closure, sequestration from the ambient world by epithelial growth over the open mesenchyme, is the final event. Several cells are crucial in this whole process of repair: platelets, mononuclear leukocytes, macrophages (transformed monocytes), angiocytes, fibroblasts, and epithelium. Acute inflammation, i.e. blood borne monocyte-macrophages are the afferent population of wound cells. Wound module is the efferent repair population made of local mesenchyme, i.e. angiocytes and fibroblasts. That is the crucial thing to remember here, that wound healing events occur via two general populations of cells – acute inflammation and wound module.

6

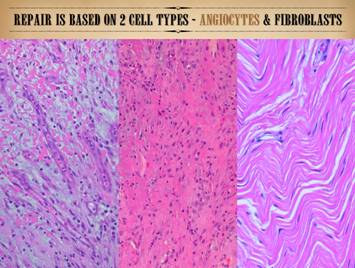
This slide is also form Part 1 of this series. It is meant to remind that the reparative population, the wound module, is made of two – and only two – mesenchymal cells, the angiocyte and the fibroblast. They constitute the repair population. Epithelium can also be considered part of the repair population, but the mesenchymal component is what figures most prominently in the process of stromal auto-immunization and the chaotic logistics of intermixed cell populations 9as will be discussed in this Part).

7

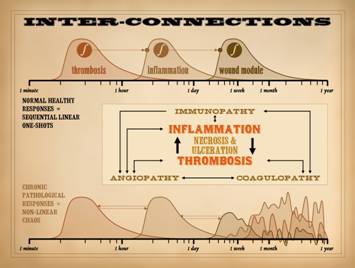
In Part 1, slide 32, and in Part 2, slide 46, we introduced the concepts of sequential one-shot dynamics and their role in the normal response to injury and wound healing. We also hinted at the nature of chaotic dynamics, and how that arises from abnormal feedbacks, dependencies, retriggers, or other sustentation of any of the system sub-phases. We also looked at how the co-dependent interplay between thrombosis and inflammation can sustain abnormal dynamics and pathology, and how they are the input hook into the system for primary pathologies to exert themselves on the wound, all with necrosis and ulceration caught at the center of this.

To refresh, recall the quintessential functions of inflammation and thrombosis. How is injury recognized? How is it cleaned up? How is the repair process started? Platelets-thrombosis are one pathway of injury recognition. Once triggered, they then initiate inflammation so the body can handle defenses, do damage control, and then clean up. Thus, (1) thrombosis triggers inflammation. However, inflammation also creates a milieu that promotes thrombosis via prothrombotic chemicals, leukocyte and platelet trapping, changes in vessels and blood viscosity, etc. Thus, (2) inflammation triggers thrombosis. They trigger each other. This complex non-linear system is self-amplifying. In the case of single incidental injury, such as trauma, this thrombosis-inflammation coupling ensures a swift ramp up of defensive changes, but then the process subsides and settles, paving the way for repair. In simple terms, trauma induced thrombosis-inflammation is a one-shot. However, when there is repetitive or sustained injury, then new thrombosis and inflammation keep getting triggered, keeping the process alive or renewed. Chronic or repetitive injury, thrombosis-inflammation triggered by a chronic hypercoagulable or micro-occlusive disorder, and acute inflammation chronically induced by immunity, allergy, or infection are the types of activities that perpetuate these events – to the detriment of the host.

It is the sustained interplay and mutual promotion of these factors which disrupts the normal dynamics of healthy repair. Inflammation triggers thrombosis. Thrombosis triggers inflammation. Many other chronic inflammatory, immune, and thrombotic disorders also trigger thrombosis and inflammation. Necrosis and ulceration are caught in the middle, making more “wound”. The orderly sequence of one-shot events is totally disrupted, becoming a cacophony of feedbacks and retriggers that keep the thrombosis-inflammation-repair dynamics in wild unpredictable states. As we will see here though, this situation might seem wild, but that is how complex natural systems really behave. This is at the heart of why chronic wounds fail, and these dynamics are understandable by studying their relevant physics, non-linear dynamics.

8

As we start to explore the physics and pathology of wounds, keep the following quintessential points in mind:

The wound module is a special ad hoc reserve organ.

It is a collection of mutually interactive self-organizing cell populations. The wound is not a pump and pipes like the heart, not a diffusion membrane like the lung, not a structural member like a bone, not a light collector like the eye, and not like any other already organized organ with an ongoing specific function. It is a collection of mutually interactive self-organizing cell populations. It has no other function than to get organized (into a generic stroma that is the foundation for other tissues and organs.)

Wound failure is a dynamical disorder of logistical self-re-organization among the wound’s constituent cell populations. When it fails, it is not an inadequate pump like the heart, not an inadequate filter like the kidney, not an inadequate bellows or diffusion membrane like the lung,

and not like any other organ that has ongoing specific function. When it fails, it simply fails to get organized into its intended final form, to complete its task to become something and then cease.

The relevant natural science which explains its quintessential structure, function, and dysfunction is physics, specifically, non-linear dynamics, including control, chaos, population logistics, and cellular automata. The relevant physics is not fluid dynamics as it is for the heart, not optics as it is for the eye, not acoustics as it is for the ear. It is the science of populations and the principles of their interaction, control, and self-organization.

When it fails, it is, in the terms of its relevant physics, a dynamical disorder of self-organizing populations.

9

The wound, the organ of repair, is anatomically and functionally a collection of cells trying to organize themselves. The relevant physics is Non-Linear Dynamics (NLD), the study of complex systems, which applies to the normal healthy wound and the failing wound. The broad subject of NLD has a variety of components. Those that will be studied here are in 3 areas: (1) the general timewise behaviors of complex systems, including control, chaos, attractors, and N-body dynamics; (2) population logistics, the study of collective and competitive group behaviors; (3) cellular automata and self-organization, the study of how deterministic rule-based systems assemble themselves with minimum information and maximum efficiency. The purpose of all of this is to explain why impaired, failing, non-healing wounds are that way, for reasons that go beyond the conventional bio-pathology of the system.

10

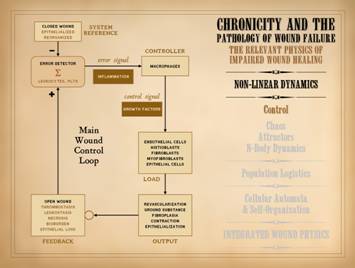
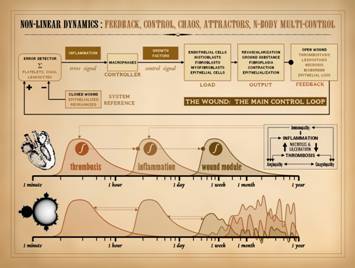
The subject of control was covered in Part 1. of this series, “The Wound as a System and a Controlled Machine”. The main wound control loop is shown here, and needs no further comment. However, it is important to understand the connection of control to non-linear dynamics. Control means feedback, to report the state of the system so that errors can be corrected. Non-linearity is explicitly defined by feedback, the system state or output at one moment becoming the input into the system in the next moment. Controlled systems are ipso facto non-linear systems. The wound is a non-linear system. The control within that system ensures that, when healthy, injured tissues return to a state of restored stromal architecture and integrity.

11

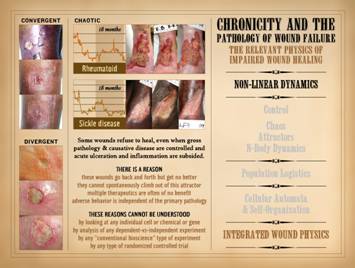
Note on slide 7 that feedbacks and sustentation of primary system triggers could lead to seemingly erratic behavior, aka “chaos”, which for the wound implies non-healing. The subjects of chaos, attractors, and N-body dynamics explain such complex or unpredictable timewise behaviors in non-linear systems. Non-linear dynamics is a modern subject, relevant only since the 1970’s – 1980’s, after the advent of digital computing. However, the basic concepts of the subject and the inherent need to have the subject have an important history over the past 300 years.

For the past 3 centuries, our main system of technical and engineering mathematics has been the calculus of Sir Isaac Newton (1643 – 1727), the mathematics of motion and change. The calculus lets you create analytical (linear) equations that describe the state of a variable versus another variable. The importance of Newton’s mathematics cannot be overstated, but the calculus does not solve all problems. Newton himself knew this perfectly well. His gravitational equation allows the behavior of two mutually interacting bodies to be described with exact precision, e.g. position, energy, velocity, momentum versus time. The problem is that the simple analytical equations which describe two mutual bodies do not exist for describing 3 or more mutually interacting bodies. Imagine for instance that you need to compute the orbit of a large moon m around planet p. Easy enough with calculus, and the results can be expressed directly as m = f(p), or parametrically as m = f(t), p = f(t). But what if it is a trinary system, with another large moon n. In that case, m = f(p), n = f(p), and n = f(m). These three mutually interacting bodies cannot be solved with Newtonian calculus, i.e. there is no general solution in the form of a functional equation. This dilemma is known as the “3-body problem”, generalized as the “N-body problem” for any number of mutually interacting objects.

For 3 centuries, scientists and mathematicians were instructed to stay away from such problems as “intractable”, and engineers had to depend on approximations and limited grainy iterations to solve real world computations. However, by the end of the 19^th century, mathematicians were starting to come to grips with the fact that complex real world systems might not be solvable with linear analytical equations, but that the real world is the real world, and that mathematics would have to rise to the challenge and find methods to describe reality. Some of the most important insights into this issue were made by French mathematician and physicist Henri Poincaré (1854 – 1912) who made seminal contributions to the subject of 3-body problems, and in so doing became the first to “discover” or anticipate the concept of deterministic chaos. The problem then though was that the iterative solutions to such problems could hardly be visualized, because such solutions depend on numerous repetitive calculations. His work, and that of other notables such as Gaston Julia (1893 – 1978) lived in abstraction and theory until automated computing in the latter 20^th century permitted the direct calculation and visualization, the “solution” of such problems.

In the biosciences, we continue to live with the legacy of “intractability”. For a century and a half, experimental physiology and biosciences have been mired in the concept of linear models of dependent-versus-independent parameters in an otherwise invariant environment. This approach to research has characterized the linear relationships of millions of cellular and chemical interactions – all crucially important, but none of that describes how systems as a whole behave (more on this on slides 15 & 16). In this, the “century of the system” (see Part 1, slide 5), and with the tools to solve iterative N-body systems, complex biosystems need to be approached for what they are – complex non-linear systems. Physicists, chemists, earth and atmospheric scientists, meteorologists, geologists and geographers, and scientists from most of the physical and earth sciences have been doing this for 20 – 30 years now. But the biosciences are largely stuck in 19^th century methods of investigation – ironic in that biosystems are far more complex and in need of such analytical understanding more than most other physical systems. The dynamics or behavior of wound healing, especially the impaired or failing wound, is a perfect example of a complex non-linear system. Classic bioscience experiments cannot explain why a wound fails, because these are problems of complex systems, for which physics – non-linear dynamics – is necessary to understand the real failures of the system. As is presented here, the failed wound, a complex non-linear system, can be understood by a several aspects of non-linear dynamics, not the least of which is that the system fails under the confluent interaction of three “bodies”, in which each body is its own complex element, a non-linear “population” of cells. It is all “intractable” according to “classic” physiologists, but it is the real world with real explanations based on contemporary physics.

12

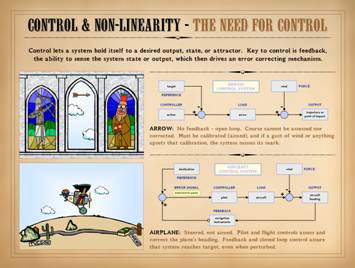
This slide is also form Part 1, Control . . . It is meant to remind that biological systems have control, allowing them to “steer” toward a desired state or system reference. An open loop system, like the arrow, requires calibration, and calibration can be upset, making open loop systems prone to error at the output. Closed loop systems, like the airplane, which can sense and correct errors, are more fault tolerant, and they can meet their mark even when perturbed.

Consider for a moment that some space alien is here on a field trip to study us. He observes without interacting, privy to no knowledge or communication other than what he can observe visually from his vantage point high in the sky. If he were to observe the airplane and pilot, what would he see? He might see a straight line of flight, from origin to destination. “Might”, because a perfectly straight path would be contingent on no winds, perfect navigation and flight control, etc. A pure straight line is unlikely, but nonetheless, the flight path will likely be nearly straight – a few minor twists, a curve here, a variance there, but still more straight than not, with a small error if fit to a regression curve. The space dude could figure out easily enough that this is a controlled flight, that variances are due to perturbations like wind or whatever, and that the pilot or system is controlling off of some basic concept of efficiency based on optimizing economy or energy on the way to the target. The deterministic rules behind the control of this system would be easy to infer, especially since the space dude himself is technologically savvy. In fact, if the space observer had sensors to observe wind velocity and direction, he could correlate those parameters with the subsequent responses of the airplane. Soon enough he would have all the data necessary to understand the deterministic rules of response, then model the system well enough to accurately anticipate the responses of the airplane to changes in the wind.

13

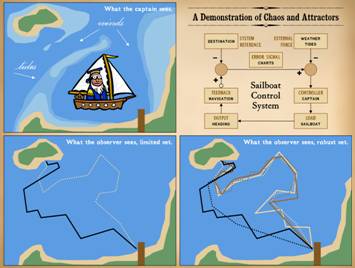
Control, determinism, and analytical predictability were all evident in the airplane control system. Now, we will look at a sailboat, in which control and determinism are equally strong, but with a more complex set of rules and responses, enough that the system state or output is not analytically predictable – aka “chaos”.

The sea captain is an experienced old salt who ferries back and forth between the mainland and the island. He has his nautical charts and an implicit knowledge of the underwater terrain. He is aware of hazardous shoals, reefs, and sandbars. He also knows of a shallow channel shortcut that is passable at high tide but must be avoided at low tide. He understands the wind and his sails, and he has complete mastery of the craft. Every trip he makes is perfect on points of safety and economic efficiency.

On the lower left, the captain has made one round trip, sailing out at high tide through the shallow channel, then taking the long way home at low tide. Tack lines vary, based on wind, water, and hazards. What would our friend the space alien see if he was observing? He might not figure this one out. He might come away downright confused about how the boat operates – i.e. what are the rules of control. First, consider that the space dude is NOT technically savvy about boats. Perhaps their planet has no large bodies of water, so those technologies never developed. Or maybe, he is an inland city boy on his home world and never took a ride in a sailboat himself. If so, he would not understand how and why the boat must tack if it is to sail into the wind. Perhaps his observational platform up there cannot sense underwater forms (sandbars) nor sea height (tides) nor the wind. Thus the space alien is unaware of these rules and perturbations. All he can see is the mainland, the island, a featureless surface between, and the boat shuttling back and forth. If the space dude assumes that the boat should move in a straight line for the sake of economic efficiency, then the strange patterns he observes will make no sense, especially if he observes just once. Yet the system is not without rules, so it would seem, because this seeming nonsensical and highly erratic not-a-straight-line-shortest-distance-between-two-points pathway nonetheless eventually converges back at the starting point.

If he took the time to observe many transits, and had a robust data set, could he then figure out the rules? No. He could theorize or hypothesize, but unless he gets direct knowledge of the underwater geography, winds, tides, and how a sailboat operates, he cannot figure out the rules. This is especially true since the response to a nearly identical set of conditions may vary, for instance a few degrees change in the wind or a week’s change in the lunar phase may make the captain take a completely different course. From the captain’s point of view, from the operational physics point of view, this system is strictly deterministic. The captain will make the same exact choices, time after time, based on explicit rules of safety and efficiency, for any given set of inputs. It’s just that the inputs are many and variable, and small changes may make a big difference in subsequent responses or patterns. If the space alien is unaware of the small perturbation which triggered a big variance in output, then the rules or responses will seem arbitrary. If the space alien makes a robust set of observations, what he will learn is that the boat sails on an “attractor”, a state space of permissible values or allowances. Where the boat will be at any given time is not strictly knowable absent knowing all of the rules (this is the principle known as Laplace’s Demon). The captain knows all of the rules. The space observer knows few of them, so he will have to infer what he can from the shape of the attractor. The complex or seeming erratic pattern of the attractor becomes very simple once you know the rules, but alas for our space friend, all he observes is apparent mayhem. This is the concept behind mathematical chaos. “Chaos” in the vernacular sense implies mayhem and arbitrariness, but in physics-nature-math, chaos is the antithesis of mayhem. It is just the complex behavior of complex or non-linear systems driven by strict deterministic rules, whether we know or not what those precise details or rules might be for a given system.

14

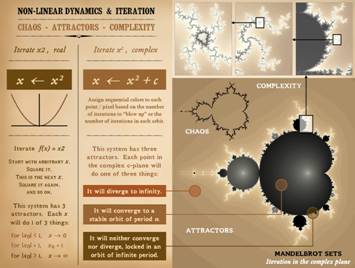
. . . All of which brings us to the point of understanding what non-linearity chaos, and attractors really are. Keep in mind that this is how all real world complex systems operate. The mathematics on these few slides is not meant to intimidate or overwhelm – in fact, just the opposite. These abstract mathematical larks are a simple way to illustrate how complex real world systems behave, starting with iterations on x².

The map (graph) of y = x² is a simple parabola. This is a linear function, a proper equation of algebra and calculus, continuous, differentiable, with a one-to-one (and “onto”) relationship between the input (independent variable) and the output. Now, let’s iterate x². x_n+1 ! x_n². Pick an arbitrary value for x. Square it, Make the answer the new value of x, then square it, and so on. What will happen. If the start value is x = 1, then the function will converge (immediately) on the value of 1. If first x is less than 1, then repetitive iteration will drive x towards zero, converging at 0 after infinite iterations. Likewise, if first x is greater than 1, then x converges on infinity. X has 3 attractors: it converges to 0, lands on 1, or diverges to infinity. The fact that the system depends on itself, that its own value or output feeds back as the input on each iteration, this is what defines it as a non-linear system. Simple enough. However, even the seemingly mundane as y = x² can become very complex when you throw in a few extra rules.

The “extra rule” here is that we will iterate x² in the complex plane. Recall that complex numbers have a real part and an imaginary part (i = square root of -1), and they must be represented on a rectilinear graph. So as to avoid the trivial attractors of zero-one-infinity, we will add a constant c, so that we are now iterating x_n+1 ! (x_n² + c). We will map the iteration in the complex c plane, meaning that every point on the grid (or display screen) is a value of c. We can then pick an arbitrary starting value of x, then iterate the equation. Depending on how the iteration behaves, we will assign a certain color to each c point or display pixel. Specifically, we will observe the values of x as we do the iteration, looking for the signs that it is going to diverge or converge. We pick an arbitrary discriminator, such as 10. As we iterate, if x exceeds that value, that is taken as a sure sign that the function will diverge, on its way to infinity. We then assign a color to that display point based on how many iterations it took to exceed the divergence discriminator. We are also looking for repetitions in the values of x as we iterate it. If a value repeats itself, that means a closed orbit has been achieved (and it will continue to repeat itself). We count how many iterations are in the orbit, then assign a color value based on that number. When we are finished iterating each point in the display field, for each value of c, what do we get? We get the amazing structure shown, the Mandelbrot set of iteration in the complex plane.

Points within the Mandelbrot set are convergent – they have settled into a repeating orbit. The closer they get toward the center, the smaller the orbit, the fewer iterations it took to find stability. Points outside are divergent – they are “blowing up” to infinity. The farther away, the faster the values are diverging, and thus the fewer iterations needed to cross the “escape” discriminator. The color bands visually clarify the structures and relationships. What is happening in between the convergent and divergent zones? If we are outside in the divergence zone, we find that the farther out we are, the fewer iterations needed to diverge. The closer in we are, the more and more iterations required to diverge, approaching an infinite number of iterations at some limit. If we start off inside, in the convergence zone, we find that if we are close to the center, then orbits converge after just a few iterations. As we move outward, it takes more and more iterations to converge an orbit, approaching an infinite number of iterations at some limit. The two zones, divergence and convergence, both take an increasing number of iterations to not do their thing as they move towards each other. At some point it takes an infinite number of iterations to find an orbit (no repetition of values). At some point it takes an infinite number of iterations to not diverge (remaining in bounds at low values). These limits of infinite iteration are the boundary between the inside convergent zone and the outside divergent zone. This transcendental boundary of infinite orbit is the “chaotic” set of this function. This boundary is of infinite complexity, which can be seen by zooming in, as shown on the upper panels.

The point is that this seemingly mundane system, a simple parabola or second order equation, can yield infinite complexity when the problem becomes non-linear. This function is highly deterministic – rule based – as all non-linear systems are. Yet the value or state of the system can be very irregular and unpredictable – aka chaotic – which leads to complexity. Even so, values will tend to be in certain permissible zones – aka attractors. The Mandelbrot set of iteration in the complex plane is a very handy way to visualize these concepts, but these are the inherent principles of all non-linear systems, including most biological systems, including the wound. The Mandelbrot set per se may not show up in your wound, but principles of non-linearity, attractors, divergence, convergence, and chaos are there all of the time.

15

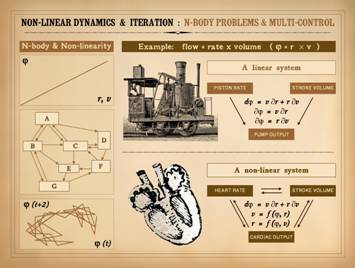
The principles of non-linearity, iteration, control, and chaos must now be extended to the subject of N-body problems and multi-control. The concept of the N-body problem was introduced on slide 11. It should be intuitive that this is relevant to the wound which has “countless” numbers of interacting cells and chemicals. To understand 3-body problems, consider the functions of a pump. The antique locomotive runs off of a steam pump. The pump has a certain flow rate, e.g. gallons per minute. The flow (p) is a consequence of the stroke volume (v) and the stroke rate (r), specifically p = vr. Engineered machines of this sort can be made so that stroke volume and stroke rate can be adjusted by the operator independently of each other. Each is an independent variable of the system, neither contingent on the other. Thus, p = f(v) and p = f(r), but v & r have no dependencies. The total flow or output varies as v and r vary. If v and r vary concurrently, you can still directly calculate variations in flow by prorating the contributions of each independent change. This is the purpose of partial differential equations: dp = v¶r + r¶v. This is a simple analytical non-linear system. Its output can be functionally graphed. Simple. Non-linear.

Next, Consider the heart. It too is a pump. Flow (aka cardiac output) equals stroke volume times heart rate, p = vr, just like the steam pump. But, there is a crucial difference between the two pumps. In the heart, as in the steam pump, p = f(v) and p = f(r), but also v = f(r). Consider a basic point of physiology: as heart rate increases, stroke volume can diminish because diastolic filling time is impaired, i.e. volume and rate are contingent. Another point: as stroke volume increases (as during exercise, due to increased venous return), ventricular stretching drives a higher heart rate, i.e. rate and volume are contingent. Each is a function of the other. There are three “bodies”, three independent variables, three mutual sets of functional dependencies. As a 3-body problem, there is no constitutive general solution to this system that lets you functionally map any one versus another nor versus time. If you want to experiment with this system, you have to iterate it.

In complex non-analytical systems, such as 3-body problems, you simply cannot state the value of a dependent variable as a function of time or some other independent variable. All you can do is say that y = f(x), x = f(z), and z = f(y). This system of three linear equations can be “solved” only with iteration. What does that mean? The method to solve the whole system is to recognize that over infinitesimally small intervals, y = f(x) is valid unto itself, and z need not be accounted for – and likewise for the other 2 equations. Thus, in each go-around, you take the current values of each variable and use them to calculate each of the three linear equations as though they were independent of each other. Then you reiterate, taking the new values of each variable and redoing the calculations. The thinner the timeslices, the more calculations you do, and the more accurate your model is (the set of equations and their one-versus-another linear characterizations), then the more accurately the iterations will mimic-model-recreate real world dynamics.

Each time you iterate, you are plugging the system values back into the system operations. This is the very definition of feedback, which ipso facto makes this a non-linear system. Such systems generally have ways to sense and monitor the feedback and compare the system state to a reference. The train engineer knows when the engine is running too fast or too slow and can make suitable adjustments. The heart “knows” when system performance is creeping out of permissible bounds and regulates things back in bounds. As we saw in Part 1, overwhelmed control or bad control can occur, but when system components are behaving properly and not over-stressed, the machine as a whole should be performing properly, “physiologically”. The heart of course has plenty more parameters that must interact than just rate-volume-flow, making it a “bazillion-body” system. The same is true for the wound. Yet within these complex systems, there are subsystems and embedded loops which each have their own feedbacks, dependencies, and regulated control. For example, in the wound, the thrombosis-inflammation loop exhibits control. The thrombosis, inflammation, and repair one-shots all have control. Even the way in which an angiocyte migrates then reassembles in response to a gradient field of VEGF is a strictly reference-driven controlled process. All of these events have “hooks” into the other control loops, acting as extrinsic promoters or inhibitors. This matrix of interconnected control loops is “multi-control”. As we have already seen, when a well behaved simple system should be acting like a one-shot, but various forces and perturbations keep elevating or rocking the system, then chaotic dynamics should ensue. With complex multi-control, chaotic dynamics is largely assured.

Remember to keep in perspective the difference between the layman’s vernacular meaning of “chaos” versus the technical meaning. The description of multi-control leading to chaos might sound awful to the naive observer, but in complex physiological systems it is a cornerstone of healthy physiological function. Multi-control is what keeps physiological systems in bounds. The moment-to-moment variability of a given parameter might seem erratic, unpredictable, and non-analytical, but the healthy system will keep that parameter within permissible bounds, within a certain “state space” or attractor. You might not know moment-to-moment what the next value or variation of a variable will be, but you will know that it stays on its attractor, unless it gets sick. Chaos, in the technical sense, is simply the way that non-linear systems will behave. There can be no other choice, no other way about it for N-body multi-control systems. The more layers of control, the more non-linearity, the more erratic the chaos, but that is the way that healthy complex systems behave. Chaos in physiological systems is not only normal, not only healthy, but if it disappears that is bad. Continuing with the heart analogy, the work of cardiologist Ary Goldberger is noteworthy (e.g. Goldberger AL. Nonlinear dynamics, fractals and chaos: applications to cardiac electrophysiology. Annals Biomed Eng, 1990, 18:195-198.) As a complex multi-control non-linear engine, heart parameters should be chaotic. If the beat-to-beat interval of the heart is finely measured, there is plenty of erratic fine variation, and this can be shown by several mathematical tools to be not just chaotic, but a consequence of control (such as the embedding diagram, left bottom). In sick patients with terminal heart disease, the beat-to-beat chaotic variability disappears shortly before cardiac arrest and death, heart rate instead becoming an exact fixed rate, meaning periodic or harmonic. Harmonic periodicity is a sign that many layers of control have gone off line. “Chaos is good, and well-behaved periodicity is bad” . . . the physics of complex systems may seem a bit counter-intuitive if you have not studied the subject. However, that is the way that healthy complex systems are supposed to behave, all a consequence of multi-control.

The straight line in the left upper panel shows a typical linear graph, such as (pump flow) = (proportionality constant) x (rate), the kind of analytical function that has governed biological research for so long. The left middle panel shows the kind of interconnection diagrams (see next slide) that characterize actual complex biological systems. Several nested or interlocked loops can be seen, and these multiple dependencies are the basis for multi-control, which will lead to chaotic dynamics. The left bottom panel is typical of the kind of mapping that must be done to see the structure in chaotic data sets, in lieu of a functional plot such as in the upper panel. There are many ways to demonstrate chaotic dynamics and attractors. The method illustrated is an “embedding diagram”, in which one variable is plotted against itself, its current value versus its value x number of iterations hence. This of course is most appropriate for non-linear systems that feedback and depend on themselves. The embedding diagram assumes that with feedback and control, the value of the system a short time from now will have a functional cause-and-effect relationship to its value now, based on its deterministic rules and physics. In making such plots, structure and attractors can be revealed.

The wound is a perfect example of complex multi-control. Chaotic dynamics are normal, but when the system is healthy, feedbacks and dependencies are minimized, and each phase or component of the process can run its one-shot event, the overall process likewise being relatively smooth and regular as it returns to the system reference “baseline” and a healed wound. When pathology and abnormal dependencies occur, the system develops abnormal degrees of feedback, multi-control, and n-body dynamics. This may be counterproductive or detrimental from a clinical point of view if the wound becomes chaotically locked into an orbit and doesn’t want to heal, but this is all normal and expected behavior from a physics point of view.

16

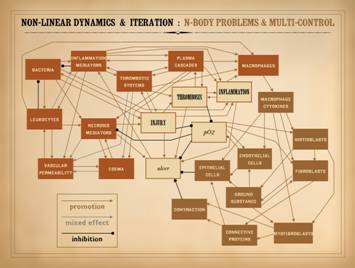
Perhaps you remember from medical school that giant chart of the metabolic pathways. Undoubtedly you have seen other highly interconnected block diagrams, such as the one shown on this slide, in a variety of lectures or textbooks, concerning a variety of topics in physiology or pathology. These charts always seem to elicit a certain mood of tongue-in-cheek irreverence, or a certain degree of apology or cynicism or whatever. There is a sense that although the author is clever enough to chart the inter-connections, that no sensible or dutiful post-doc would ever actually design an experiment based on such a jumble, nor would any self-respecting bioscientist ever attempt to derive from such a mess a unification theory that would explain integrated metabolism or pathology based on such a briar patch of blocks and arrows. Yet this is the real world, real physiology based on real dynamics. When a wound fails, or there is unexpected worsening or improvement, or there are contrary responses to therapy, the reasons need not be a matter of confusion. The understanding of such situations is built into these interconnection diagrams, once you start to understand how the elements in such systems inter-operate.

In the example shown, a variety of elements relevant to wound physiology and pathology have been inter-connected. This is non-rigorous, with an arbitrary selection of relevant (but generally important) elements. Red items pertain more to injury, acute inflammation, and afferent wound events. Brown blocks pertain to efferent or reparative events. The ivory blocks in the center are major states or common elements. They have a multitude of interactions, either promotional-stimulatory versus inhibitory versus mixed effects depending on circumstances. The numerous blocks qualify this as an n-body system. The varying patterns of feedback create complex multi-control, with individual loops nested, intersected, and inter-connected. Classic bioscience experiments have studied and published the parameters, equations, and coefficients that characterize the interactions between any pair of elements. Each 2-body pair has a strictly deterministic profile. But as was seen on the last slide, the mutual inter-dependence of many elements in this system means that system state or output will have complex non-analytical non-functional non-harmonic patterns, i.e. chaos.

This graph was made arbitrarily – relevant but generally important items were selected until space ran out. Then, the blocks were connected to others based on common knowledge and principles of inflammation, wounds, cell biology, etc. But in looking at the overall result, notice something interesting. There are few inhibitory lines. In fact, the three early state events – injury, thrombosis, inflammation – have no inhibition whatsoever. This was not an intentional design goal, not a deliberate artifice, not a rhetorical device to prove a point. The control elements were interconnected according to basic knowledge, and guess what – no suppression of injury, thrombosis, inflammation. We can suppress them therapeutically, but the natural system needs no suppression. These events extinguish themselves – they wind down and dissipate on their own as long as they are not re-triggered or flared up. This dynamic sits at the heart of why healthy wounds heal, and why they do not when wound chronicity sets in.

17

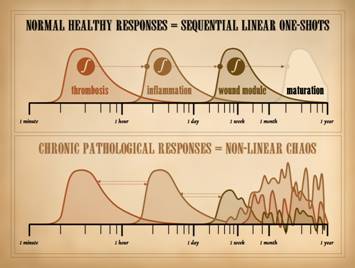
This slide comes from Part 1. of this series, “The Wound as a System and a Controlled Machine”, slide 32. In looking at wound repair as a controlled machine, we saw that when the system is healthy, the tissues can return to baseline status, i.e. heal, along a smooth trajectory that indicates good control. If we are more precise and look at the distinctive states of the wound – injury (then) thrombosis (then) inflammation (then) wound module (then) maturation – we see that each state has a smooth ramp up then decay, a one-shot. Each state is well controlled. Each state decays and dissipates as its own respective control loop succeeds in restoring its own sub-system to stability or normality. Direct suppression or inhibition from the outside is not needed. This is inherent in the principles and mathematics of control. This is how the healthy wound behaves, from injury to healed.

We also introduced the concept that each of these major states acts as some sort of trigger (generally an integrator or threshold switch) to turn on the next major event in the sequence. As long as the system is healthy and nothing re-triggers it, then these major states act as a series of one-shots, separated sequentially in time, and even separated in space, as we saw in Part 2, “Auto-Immunopathy and the Intrinsic Disease of Wound Healing”, slide 52. However, under conditions of repetitive or sustained injury or pathology, then abnormal feedbacks, retriggers, or other sustentation can occur, either sustained forward-stimulation of the downstream event, or backward-stimulation of more acute events. In Part 2, we saw the various reasons why the pathological wound is subject to abnormal sustentation and perpetuation. These conditions of sustained injury or disease result in feedback, multi-feedback, and n-element interactions. The dynamics of the output will seem erratic and unpredictable, even though they are highly deterministic interactions – i.e. chaos. We have now seen here in Part 3 what is really meant by chaos and how it occurs. It should be no surprise then that wound dynamics will be chaotic when anything upsets the orderly series of one-shot events that characterize straight-and-narrow healthy wound healing in healthy systems.

18

The main wound control loop reduces the wound module to its quintessential dynamical elements, making the principles of feedback and control, the basis for non-linearity, easy to see. The Mandelbrot set of iteration in the complex plane is an easy way to illustrate the complexity or chaotic behavior that can arise from very simple rules and recursion (feedback). In complex physiological systems, the elements of feedback and control, non-linearity and complexity become more elaborate and multi-layered, such as for the heart where even a rudimentary concept like pump output becomes a three-body problem. What it all means is that absent a detailed knowledge of all rules and parameters, it is impossible to predict or calculate with exact precision what the values of parameters will be in moments to come. Yet it is easy enough to know where the general attractors of the system are, i.e. what its permissible state space is, and what the general dynamical behaviors or responses of the system will be.

For the wound, with all of its complex physiology, yet with basic feedback and control, its state space can be reduced to three attractors: the healthy wound, the sick wound, and the impaired wound. For each, there is: (1) a tangible or gross state that can be observed; (2) a physical state of the machine and its parts; (3) a teleological state, a state of intent or goal or heading; (4) a dynamical state, the activities or state of the control loop. From this point of view, the three attractors can be characterized as:

The healthy wound. Tangible state: the wound that is actively healing. Physical state: the wound module is healthy and competent, functioning properly. Teleological state: the wound is getting better and closing. Dynamical state: the wound is convergent, it is settling toward a stable or resolved state.

The sick wound. Tangible state: the wound is actively pathological, feeling the effects of active injury, disease, thrombosis, and induced or applied inflammation. Physical state: active injury and ulceration are occurring, with inflammation-lytic or thrombo-infarctive forms of necrosis. Teleological state: the wound is getting worse, actively ulcerating and getting bigger. 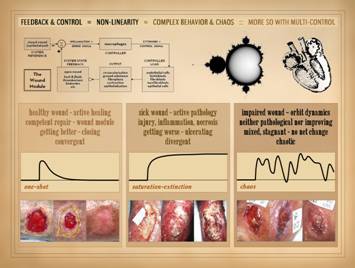Dynamical state: the wound is divergent, “blowing up” to large values of area and pathological histology.

The impaired wound. Tangible state: the wound is in a go-nowhere state of incidental back-and-forth with no real progress, “orbiting” in the same sense as the underlying dynamics. Physical state: the wound is neither pathological nor improving, i.e. disease (the sick divergent wound) is arrested but the wound remains not healing. Teleological state: the wound is neither getting better nor getting worse, with mixed features from one observation to the next, but overall stagnant with no net change over long intervals. Dynamical state: the wound is chaotic, on the cusp between divergence and convergence, orbiting endlessly until some strong perturbation can knock it to one side or the other.

19

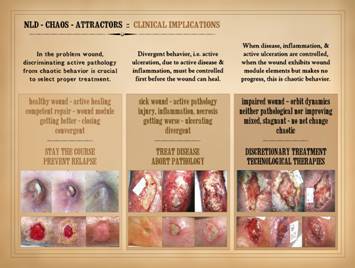
On the last slide, we summarized the implications for the wound of non-linear dynamics, chaos, and attractors. Here, we can translate that into clinically relevant information relating to wound diagnosis and therapy.

Remember, the wound can be in one of three states. It can be healthy and getting better. It can be sick and getting worse. It can be impaired and just not going anywhere, no longer sick but not yet getting better.

Proper diagnosis is the keystone to all good care. Without a correct diagnosis, proper treatment cannot be selected nor managed. Among the various constituent elements of a thorough wound diagnosis, one is the dynamical state of the wound, and the clinician MUST be able to distinguish or discriminate active pathology from chaotic behavior. We have at our command many therapeutic tools to treat problem wounds, Some are tools to treat underlying disease, and some are wound therapies to stimulate an impaired or retarded wound. Without discriminating active disease from dynamical “lethargy”, wrong treatments will be selected and care will be wasted or the patient harmed. For example, in the actively pathological sick wound, applying expensive stimulatory therapies such as recombinant growth factors or cultured living cell products in the face of active disease and acute inflammation is a profound waste of time, money, and resources. For the chaotic impaired wound, boosting steroid doses (e.g. for a rheumatoid wound) after immunopathic inflammation has already subsided is wasteful and potentially harmful.

Divergent behavior, i.e. active ulceration, due to active disease & inflammation, must be controlled first before the wound can heal. When disease, inflammation, & active ulceration are finally controlled, and the wound starts to look healthy, but it then makes no progress, this is chaotic behavior. These two states, divergence versus chaos, active disease versus non-healing, must be discriminated in order to choose correct treatment. Most experienced wound clinicians understand this implicitly. It is the purpose of these papers to clarify that when the wound should be healing but isn’t, that this is a thermodynamically stable state, and there is a basis in physics for this situation. Understanding this is necessary to have greater equanimity in your approach to the wound and the patient, and to become more exact in choosing treatment.

Remember, as an organ the wound is just a collection of cells doing interactive things. If the correct treatments are to be chosen, then its diagnoses must reflect the behavior of cell populations – i.e. non-linear dynamics and population logistics. It is the same as the diagnosis of heart failure (pump with valves and pipes), where valvular dysfunction, ventricular diameter, wall motion, ejection fraction, diastolic dysfunction, cardiomyopathy, rhythm, and cardiac “fuel” (coronary supply) are all crucial to the thorough diagnosis and selection of treatments. For the cardiologist, nuanced differences in these parameters can make differences in choice of treatment. For the wound physician, understanding the dynamical states of cell populations is required to understand the status of the wound and pick proper therapy. For the three general attractors or states of the wound, the following are the major therapeutic imperatives:

The healthy wound. (Active healing, competent wound module and repair, getting better and closing, convergent.) “Stay the course.” Continue current therapies, and make sure that there is no relapse or recurrence of primary disease or injury. Therapies may be basic and passive, non-specific general care to keep an intrinsically healthy wound healthy, or they may be discretionary or technological therapies that have successfully turned the wound from an impaired non-healing state to its current healing status.

The sick wound. (Active pathology, with injury-inflammation-necrosis, getting worse and ulcerating, divergent.) Treat the active disease or injury, and abort the pathology. Ameliorate or mitigate additional risk factors and stressors. Get the wound under control, without active inflammation, necrosis or ulceration, without symptoms nor threat to general health. Deliver the wound to a state of healing (the healthy wound) or at least neutrality (the impaired wound).

The impaired wound. (Orbit dynamics, neither pathological nor improving, mixed-stagnant with no net change, chaotic.) This is the time for discretionary treatment, the time to select specific and directed therapies meant to force the wound to close or to implement some other definitive plan of care. At one end of the spectrum of options, this might be a deliberate choice to accept the impaired status of the wound and treat it chronically as open, with basic hygienic care to avoid relapse. At the other end of the spectrum, this might be surgery for immediate closure. Or, the choices may come from the middle of the spectrum, intermediate technological therapies meant to stimulate the wound to heal, to force it onto the convergent attractor, including pharmaceuticals, biologics, and physical and machine-based modalities.

20

As a machine, as a non-linear system, as a system subject to control and chaos, there is a final aspect of chaotic systems, including the wound system that must be appreciated – thermodynamics. As we have seen through just a few introductory examples or equations, non-linear & chaotic systems can have stable attractors. A system tends to dwell or return to that attractor, unless some major upheaval forces it onto another attractor. Attractors can be thought of partly as gravity wells or charge wells, a big planet or a small ion that other objects want to orbit or fall into. Consider for example a planet with a satellite. The satellite has kinetic energy that keeps it in orbit. Alternately, our friend the space alien might have some technology to arrest the motion of the satellite to otherwise keep it suspended in a given position, in which case the object has potential energy, ready to be converted back to kinetic energy as soon as it is allowed to drop. If the object drops, or if its orbit decays, then the system is giving up energy, and the orbit and objects are converging. The space dude could also turn on his thrusters, put energy into the system, and elevate the orbit via increased kinetic energy, even to the point of escape velocity, i.e. divergence between the objects. Between convergence and divergence are orbits of variable period, depending on the energy in the system. This is no different than the attractors and dynamics of the Mandelbrot set.

All objects have a certain basal energy. (Their mass per se is also energy, E = mc², but that is not convertible to anything else under common everyday circumstances and need not be further considered.) They have an obligatory amount of energy due to temperature and pressure. This Kelvin energy cannot be converted to anything else without giving up heat. It can be transferred to other objects, but if any of it is lost, then the temperature of the body diminishes. Closely allied to this basal energy is the concept of entropy, the amount of heat gained or lost at a given temperature. Entropy will always increase in the “downhill” transfer of energy, so it reflects conditions of equilibration or convergence. Objects can also have “free energy”, additional energy beyond their Kelvin temperature (Gibbs energy). It is “free” because it is readily convertible without changing temperature or entropy. This is kinetic energy and potential energy, as stored in the separation of gravitational or charged objects, or in the elastic deformations of a spring, or in the bonds of an energetic molecule. For the orbiting satellite, free energy is kinetic. If it sheds free energy, its orbit decays. If it gains energy, its orbit is elevated. If an elevator is stuck on the 5^th floor, it has a certain amount of free energy stored as gravitational potential energy. If it goes up, more free energy must be put in to elevate it. If it descends, it sheds free energy. Total system energy for an object is its enthalpy. Its obligatory basal energy due to heat and pressure is its kelvin energy. The difference is the free energy which is convertible and reusable.

Consider an ideal spring or clock pendulum in motion, or a satellite in orbit. The oscillation rate of the spring and pendulum, and the height or period of the orbit will depend on how much free energy is in the system. However, if it is an ideal perfectly elastic or conserved system, then it oscillates or remains at altitude without needing new energy (except to replenish whatever little is lost “internally” due to friction and the like, e.g. the clock pendulum needs a wound spring or weights). Nature and engineered systems are full of such systems where, except to replace internal losses, no other energy is needed to maintain motion or current state. Motion continues ad infinitum, because no free energy is dissipated or transferred to another object. But if free energy is added to or removed from the system, then system dynamics change, such as oscillation rate or height or period of an orbit – the orbit goes higher or the clock ticks slower. However, although certain dynamics in the system are free energy dependent, others are not. If one records the motion of the system, complex forms or morphology can arise, passively and without the expenditure of energy. A Lissajous figure forms from a swinging pendulum without requiring energy, and a clockface sweeps out overlapping harmonic circles. Now, consider the grass-sheep system. (This is discussed as part of population logistics on slide 23. You might want to read the next few slides, 21-22-23, then come back here to finish this slide.) Grass mass is converted to sheep mass via magic sheep enzymes, and sheep mass is converted back to grass mass by magic fertilizer made by the sheep. It is a closed system of fixed mass that flips back and forth between different levels of grass or sheep. It is also closed in that no energy is transferred outside or to other entities, and thus no new energy is needed to run the system other than some sunlight to refresh internal losses. The system is inter-convertible between grass and sheep just by letting the system follow its own rules, letting it “oscillate” so to speak between grass and sheep. Of course, the system does not really oscillate – that would be periodic or harmonic motion – very linear or non-chaotic. The whole point of the non-linear logistics map was to show that the sheep-grass partition will vary in complex ways that need to be iterated to see the moment-to-moment values. So, it does not oscillate, but it does go “back and forth” in its own way, which could be construed as an elastic interaction of sorts, or an orbit of sorts (which is why we refer to those attractors as orbits). Even though chaotic non-linear systems move in ways that are not harmonic and cannot be explained by Newtonian calculus (such as by a spring or gravitational equation), nonetheless the same thermodynamic principles apply. When a chaotic system is in a stable orbit, it continues on that chaotic attractor in the same way that an ideal spring (without internal energy dissipation) stays in its harmonic oscillation without needing new energy inputs. It is easy to understand that if I want to boost satellite orbit or spring oscillation, I need to put free energy in, by thrusters or stretching. For chaotic systems, changes of state and transitions between attractors can be increased by putting force or perturbation in from outside stressors, thereby adding energy to the system. And just like for a Lissajous figure, chaotic attractors can also have complex morphologies that may not be energy-dependent (e.g. the bifurcation maps, cobweb diagrams, and “mandeloids” seen on slides 14 & 23). These patterns and morphological complexities are more a matter of the feedbacks and controls in the system, more a result their intrinsic or internal elements, rules, and dependencies. These are the “wave shapers” in the system, rather than the free energy, a matter of how the free energy is routed within the system rather than how much is applied to or withdrawn from the system. As an example, I could regularly add an unnatural new fertilizer to the grassy field, something that promotes grass growth, but also makes it unpalatable to some of the sheep. This is a perturbation from without (equivalent to adding or subtracting energy) which will markedly affect the dynamics of the system, fundamentally altering the grass-sheep balance and shifting the chaotic attractor of the system. Alternately, I could just change the time of day that the sheep are unpenned and allowed to feed. This change in the internal rules (equivalent to neutral energy redistribution only) might very well change some of the precise iteration-by-iteration values of the system, but the general forms and morphologies of the attractor, and especially its basins, moments, and “centers of gravity” are unlikely to change.

In chaotic systems, including the wound and any other complex or non-linear physiology, the system will move from one attractor or orbit to another, or converge or diverge. Trans-orbit or trans-attractor shifts, or convergence or divergence, are equivalent to adding energy to the system, or taking it out. When a system is stable on an attractor, it has no net gain in energy or information. Thus, attractors are like basins of stability, and the system will break away only if enough energy is put in to elevate it above threshold. The concept of basins or wells of energy stability are of course common in nature. Consider certain exothermic chemical reactions or a nuclear fusion or an action potential in a nerve or muscle cell. An activation energy is required, something to boost the system to its threshold or trigger point, and then reaction is autonomous, releasing large amounts of free energy from broken bonds. The system has to go “over a hump”, taking a bit of added energy to climb over, then yielding much larger amounts as it slides downhill, just as if it was falling in a gravitational field and giving up potential energy. Of course, once the system has settled into its new basin, there is no going back, at least not easily. If the reaction is nominally reversible, all of the dissipated energy has to be put back in again to boost it up over the now much higher hump. When chaotic systems hit stable attractors, it is as though they have gone over such an exothermic hump, giving up free energy, finding it “easier” to dwell where it is rather than move to another state or attractor. 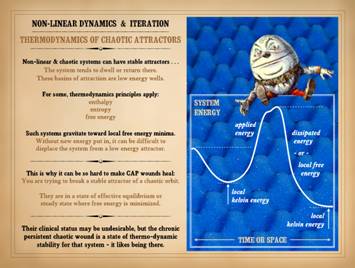Energy inputs by extrinsic stressors are what can elevate the orbit again, and when the stressors are relieved, the system can settle back into whatever attractor or basin it can “thermodynamically” – or just plain “dynamically” – occupy for the current conditions.

Chaotic systems are generally not in equilibrium nor steady state, but it can seem that way, or it can be defined that way. When a logistic map settles into a bifurcated 2-value state (i.e. for A=3,25 on slide 23), that certainly could be a valid instance of equilibrium. Any n-value orbit that regularly returns to its multiple values could also be defined that way if you choose. Of course, for a long-orbit attractor, you may never see the return to base value, and not ever for a converging or diverging system. For chaotic non-linear systems, the general dynamics are different than equilibrium or steady state, but they can be loosely associated for certain circumstances. Low energy wells and stable basins of attraction will seem steady or equilibrated when the system refuses to budge – like for a chronic wound that never really changes regardless what you do. When a chaotic system “gets stuck” in a low energy basin, it has effectively undergone an exothermic reaction, giving up free energy, dwelling at a point of low kelvin or basal energy. These basins are local minima, either in time or space: (1) time, the system may dwell there for a certain time, then applied energy or perturbations break that cycle and lift the orbit, or (2) space, in a complex system like the wound, there are zones and strata and fluxes that may make one area be in a state different than a neighbor. When the system has found a stable attractor or energy well, it can be difficult to displace it. This is why it can be so hard to make chronic and pathological CAP wounds heal. You are trying to break a stable attractor of a chaotic orbit. The system, the impaired wound, is in a state of dynamical stability where free energy is minimized, and displacement from that basin of attraction requires new energy or perturbation from the outside. Obviously, if the system with its own closed set of elements or actors has found a stable dynamic and wants to dwell there on a closed repetitive orbit, it just simply isn’t going to go to another orbit on its own. Some player from the outside must come in and persuade or force it to do something different. Those forceful outside players are the deliberate therapeutic interventions that are prescribed and administered for the sake of trying to cure the wound. For auto-immunopathic ulcers, where the wound has become “intrinsified”, simple dressings, hygienic care, and basic wound healing dependent surgical repairs are not sufficiently forceful to raise the orbit or break the attractor. The forceful interventions which can change attractors are the pharmaceuticals, devices, and other modalities which suppress the primary disease, used in partnership with potent technology based wound treatments such as stimulatory and regenerative therapies. It is important to understand that for chronic pathological wounds, their clinical status may be undesirable, but the chronic persistent chaotic wound is a state of hard-to-break dynamical and thermodynamical stability for that system.

Humpty Dumpty, illustration by English illustrator Sir John Tenniel (1820 – 1914), for Through the Looking Glass by Lewis Carroll (chapter vi). Illustrating the concept that “you can’t make a chicken from chicken salad”, Humpty’s great fall epitomizes the difficulties of sliding down an energy well – falling into a stable attractor – and not being able to climb out so easily, not even with all the king’s horses and all the king’s men.

21

It should be clear by now that dynamical or thermodynamic stability may be in synch with or at odds with clinical desirability, but that a sick ulcerating wound is nonetheless a stable attractor. This raises the inevitable question, why then does the CAP wound get into a state of dynamical stability even if that state is counter-productive to health? If the control loop is supposed to work toward restoring a reference, why does it become complacent about an unconverged status? This has already been answered in part – it is inherent in the principles of non-linearity, chaos, and attractors. 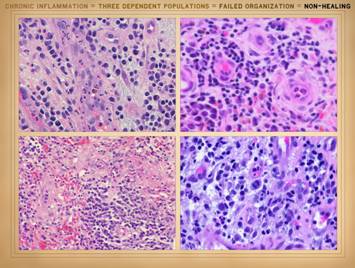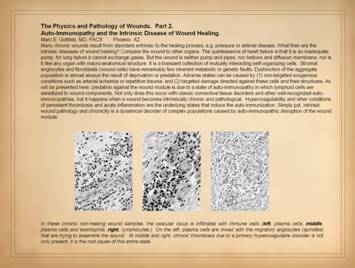At this point though we need to acknowledge the actual physical structure or biological components of the wound. It is a set of cells. In Part 2 we saw that when wounds become auto-immunized and pathological, that the normal two cell populations of the healthy wound, acute inflammation and wound module, are joined by a third population, chronic inflammation. 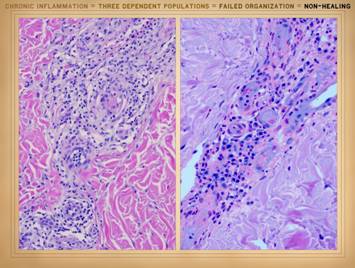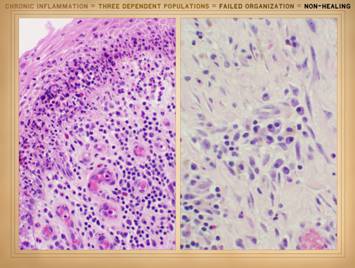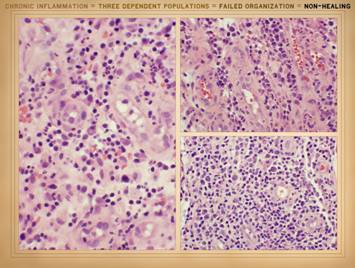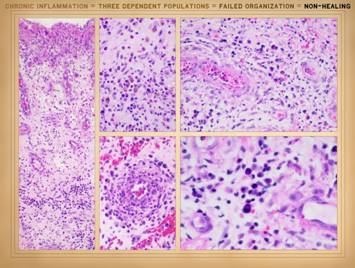As we discussed on slides 2 & 3 of this section, the wound as an organ is defined by its cell populations. To understand how these populations interact and either succeed or fail to restore a stroma, we must now look at another aspect of non-linear dynamics: population logistics.

22

Understanding population dynamics starts with understanding its simplest scenario, a single population whose growth is limited by available resources. First, think about population growth intuitively. You start with a small number. They reproduce. Their descendents reproduce. If within a given time interval there will be a consistent fraction of the population which spawns, then in each time slice population increases by that percentage. For example if population is P and growth rate is r, then P_t1 = rP_t0. After n iterations, P_tn = rⁿP_t0. This obviously is a form of exponential growth. To be more formal and continuous, dP/dt = rP, the solution of which is simply P_t = P_oe^rt. The problem is that in the real world, there are few opportunities for a population to undergo totally unconstrained exponential growth. Resources will be limited – space, food, whatever – and this will slow growth until the population’s resource utilization matches the resource supply rate, or until it has occupied the available space. The simple concept of exponential growth has to be modified to account for resource limitations. The subject is called population logistics, and in its simplest form, it derives from the Verhulst equation.

The Verhulst equation (aka logistics equation) concerns a population in which space or substrate supply is limited, meaning that the population can grow only to a maximum. If substrate supply remains constant after achieving the maximum population, then the population stays there, new individuals replacing those that are lost, a steady state. If substrate supply rate starts to dwindle, then the population will start to decline, the curves going down in reverse of the uprise. Let us focus on the uprise. The curve starts out quickly, because a small population has a lot of space or resource to grow into. As the space gets more crowded, there are more citizens and fewer free resources, so growth rate must slow. Eventually population caps out at the maximum sustainable. Intuitively, the curve should be sigmoidal or plateau-like. That is in fact what happens. Start by defining P = actual population, K = maximum permissible population (“capacity”), and r = maximum possible growth rate (the intrinsic reproduction rate if there were no resource constraints). The population will grow according to dP/dt = r P (1 - P/K). This means that the change in population per time is proportional to three parameters: (1) the existing population P (the basic predicate of unconstrained growth); (2) the space available for new population to grow into (1 – P/K) (remember, P/K is a fraction less than 1); (3) the intrinsic growth coefficient r. [ The analytical solution of this equation is a simple integration. The trick to doing this integration is to do a preliminary transform on the equation. Start with dP/dt = r P (1 - P/K). Next, divide both sides by K: dP/Kdt = (1 - P/K) rP/K. Now, define x = P/K (this value is the population fraction, the portion of total capacity that is currently populated). The equation is now dx/dt = rx(1-x), which can be integrated easily. ] Notice the dynamics of this equation. When x is small (early population), then (1-x) is nearly 1, and the growth rate dx/dt is close to rx, the unconstrained maximum rate. As population matures, (1-x) governs the values, and as x nears 1 (available space nearly full), then (1-x) approaches 0, and growth ceases. The slide shows the Verhulst equation graphed for various values of r.

The Verhulst equation as just presented is linear – i.e. continuous, differentiable, and a true function of a dependent value (population) mapped one-to-one onto an independent variable (time). It tells you the population as a function of time. It is orderly, because it has no dependencies other than time. The key stipulation for using this equation is that the growth system has one population that is resource limited. As shown in the next slide, the dynamics get more complex as multiple populations appear and compete with or otherwise influence each other.

23

The Verhulst equation describes intrinsic population dynamics, but the way it applies or behaves changes as the system gets more complex. Population levels and behavior become very interesting when additional populations, population dependencies, and resource restrictions are put into the system. To illustrate, we will start with a simple scenario. Consider a big field full of grass with some sheep. The sheep eat the grass, grow strong and fecund, and beget more sheep. If the grass maintains a fixed mass year by year, then there will be a maximum number of sheep that can be supported, and the sheep will grow into this fixed resource “space” according to simple Verhulst dynamics. What happens though when the resource supply rate is not fixed, in fact it competes with the sheep? How? Let us “close” the system so that there is a fixed biomass divided between sheep and grass. This means that the grass mass decreases as sheep mass increases. Eventually, the sheep outgrow the available grass. The sheep population will then start to decline, and as it does, grass mass again increases. In this scenario, the grass is not supplied at a fixed rate. The grass is an active population itself, just like the sheep, and it can be depleted but then it can rebound. Sheep and grass are two mutually interlocked populations, at times supportive, at times confrontational. Nutrition, starvation, predation, cultivation are the intertwined dynamics. The problem gets even hairier if you then throw in a third element such as wolves to eat the sheep. In this scenario, can we calculate the population of sheep or grass as a matter of time? Not so easily. The Verhulst logistical equation still applies in principle, but now it must be applied to two populations, and those two are contingent on the other! The balance between two interactive populations cannot be calculated by a continuous linear equation, because this has now become a “non-linear” problem, the heart and soul of real world complex systems. There is no way to calculate, as a direct analytical function, how many sheep or how much grass is there, neither one as a function of the other [ sheep = f (grass) ], nor parametrically in time [ grass = f (t); sheep = f (t) ]. Nonetheless, this problem can be solved, but as for any non-linear complex system (aka non-linear dynamics) the problem is solved by recursive iterations, using the iterative form of the Verhulst equation, the “logistic difference equation” x_n+1 ! Ax_n(1-x_n). Notice that it is still the logistical equation, with x being sheep, and (1-x) still being the space available for sheep to grow into. However, (1-x) is also grass, and grass is an independent population, and from the grass point of view, grass is the dominant variable g, and sheep are just the available resource (1-g). Growth rate A is also present.

It turns out that the dynamics of this system, the amount of sheep or grass, has a very strange and wonderful set of back-and-forth numbers iteration by iteration or year by year. The table shows iterates for various values of A. (Note that this table was created on a spreadsheet. For anyone interested in this subject, these equations can be experimented with using tools that most likely are already on your desktop.) When iterated, the value of x will do 1 of 4 things (depending on the value of A): converge to zero, diverge to infinity, enter an N-period orbit, never settle (chaos). See how this is similar to the behavior of the Mandelbrot? This is the general behavior of non-linear systems. Notice that at lower values of A, the iterates will wander through a few values, then converge to a fixed value, e.g. for A=1.50, x stabilizes on 0.333 (a 1-period orbit). As A values increase, it takes more and more iterations to converge to a fixed value. After that, the values bifurcate, flipping back and forth between 2 values, e.g. x = (0.496, 0.812) for A = 3.25. At yet higher A values, the orbit bifurcates again. Amazing, but that is the way it really works. The bifurcation diagrams in the center map the orbit values versus A. What is obvious is that a simple iteration like this can lead to intricate complexity and seeming mayhem, i.e. mathematical chaos. On the right are cobweb diagrams that map the sequential values of the iteration on a graph that has the linear form of the equation (parabola) and the identity line. These show that although values may jump around erratically on a large orbit, that nonetheless they stay bound to a well or basin or attractor or compact state space. Population dynamics are deterministic and chaotic, but not random. Compare this to the boat captain and his alien observer (slide 13). If you know all details and parameters of the system, you can calculate the next iterate. If you are not LaPlace’s Demon and do not know all relevant information, you can still observe the general attractor of the system and the limits of its allowable values, but you cannot be certain what the precise next value will be.

Now, consider that these two complexly interdependent populations, grass and sheep, were spatially separated at the start. Suppose that the first few sheep were confined to just a corner of the field, and that they stayed in their corral because there was more than enough grass in that corner to meet their needs. However, as the population increases, then in their quest for food, the population will migrate outward to greener areas. Whether by random wanderings (aka random walks or diffusion) or by taxis and tropism (explicitly drawn to the greener pastures), the sheep eventually spread through the field. If they were meant to stay separated when sheep population was small, that sequestration falls apart as time, population growth, and diffusion progress. Now, compare this principle of diffusion and admixture to the events that occur in the wound, when inflammation is sustained, and the inflammation and repair populations get mixed in time and place.

Grass-sheep or wolf-grass-sheep are not meant to be strictly analogous to the wound and its 2 or 3 populations. For instance, the wound is not a fixed biomass system as the grassy field was. Relationships might seem reversed or counter-intuitive, e.g. lymphoid induction of acute inflammation is bad clinically, but it is a promotion-cultivation event between these populations. Nonetheless, for both of these systems, the core principles of non-linear logistics apply. For acute inflammation, wound module, and lymphoid inflammation, their appearance, uprise, then decay follow Verhulst dynamics. When their intermix dynamics become chaotic, then the value of any one of the populations varies in complex ways. However, the chaos and complexities merely reflect the dependencies or contingencies that develop and feed back between these populations: predation, deprivation (starvation), cultivation, sustentation (nutrition). They can promote each other, compete with each other, starve-attack-inhibit each other, cultivate or nourish each other. The physical realities of wound versus grass-sheep may be different, but their dynamical physics are the same. The main message is that in these complex systems of interacting populations, the dynamics can be strange, seemingly unpredictable, and at times locked in to “attractors”, states of being, from which it is hard to break away. The physics of non-linear dynamics explain that this is the normal natural behavior of complex interactive populations.

24

The application of population logistics to the wound was implied in the last paragraph. This slide looks at wound logistics for the healthy one-shot wound.

Healthy physiologic wound healing is initiated by injury & thrombosis, then conducted by two cell sets, acute inflammation & wound module. It is a sequence of one-shot self-completing linear events: primary injury & thrombosis, then acute inflammation, then wound module. The sigmoidal rise and fall of each population shouldn’t be surprising. These populations, acute thrombosis, acute inflammation and wound module start from zero, no population. Their precursors are there, but the activated species are not. Once activated, they beget more of themselves. Thrombosis begets more of itself by auto-amplification and recruitment of more precursors. Acute inflammation (leukocytes) beget more of themselves by recruitment. Angiocytes get more of themselves by mitotic proliferation. For all, the dynamics are sigmoidal, fast on the uprise when amplification is largely proportional to extant population, then topping out as primary triggers or inducers decay, equivalent to a reduction in a vital resource. The downslope occurs as triggers completely disappear, a time lag or phase shift between the triggers and the response of the population, but still sigmoidal-Verhulst.

Each of these events or populations is an integrator function to trigger the next population. As each decays, it stops inducing the next, so then the next population starts to decay as well. When the system is healthy and injury is incidental or self-limited, then the reactive events are non-competitive populations that barely overlap or “see” each other. Each compartment triggers the next, but there is no feedback to sustain or re-trigger events. Because there are no feedbacks or sustentation, then the overall dynamics avoid complexity, recursion, and instability.

25

We now look at population logistics in the pathological wound. Pathologic wound healing occurs when sustained injury, population persistence, non-linear feedback, & abnormal population dependencies sustain the activity of any or all of the primary compartments.

The persistence of the primary disease or injury can obviously be a cause of sustained abnormalities. If the disease is sustained, then the response of the subsequent compartments is to get “smeared out”. They will extend in time, and their populations will increase under the effects of the continued induction or stimulation. The compartments will get increasingly admixed or exposed to each other as time goes by, both overlap in time, but also admixture in the strata of the wound. If the problem was just a matter of continued primary injury, then the outputs would still be linear. The populations of acute inflammation and wound repair could be calculated from (1) the transfer function or relational equation that defines the response (dependent variable) to the injury (independent variable), and from (2) the deconvolution of the output that can separate values related to a “smeared out” input. The whole system would be sustained as long as injury is active, but the dynamics would be relatively smooth, well-behaved, and related to the input. Inflammation would subside (Verhulst) and then repair would complete itself (Verhulst) as soon as primary injury was relieved.

The real problem is when feedbacks develop that “chaoticize” the system. Remember the circular relationship between thrombosis and inflammation, and their effects to make new wound which can then further promote the system: injury -> thrombosis -> inflammation -> injury -> etc. etc. etc. Once sustained injury leads to sustained inflammation, then these cycles feed back to stimulate their antecedent events. Once this happens, then the system state or output loses all functional relationship to the input – i.e. it is chaotic. The dynamics of this mix include a variety of promotional and inhibitory effects between populations and compartments. These are the “negative” population dependencies which will tend to promote or sustain the pathological state, making it harder for the system to settle back to its linear Verhulst dynamics and thereby heal the wound. The nominally normal 2-population wound (acute inflammation and wound module), can therefore develop non-linearity, persistence, and chronicity if primary injury or disease are sustained. As discussed in detail in Part 2, “primary injury or disease” can be any condition of repetitive or sustained trauma, inflammation, immunity, allergy, infection, thrombosis or micro-occlusion, etc.

These dynamics worsen when pathology, negative dependencies, and chronicity eventually induce a 3rd population of cells, lymphoid inflammation, aka “chronic inflammation”. This has the effect of taking an already chaotic 2-body problem and turning it into a 3-body problem, further complicating the mix of mutual promotion, inhibition, and competition. (This is like going from grass-sheep to grass-sheep-wolves. If one considers thrombosis to be its own population in this mix, then it is a 4-body problem.) This complex mix of dynamics cannot land or converge, consistent with the non-linear form of logistical dynamics (the logistic difference equation) rather than the linear form (sigmoidal Verhulst). As we will see soon, this third population is an autonomous negative influence on the system, acting as a sustained primary injury. Even when initial disease or injury is then eliminated, the effects of the third population are comparable, maintaining the chaotic dynamics that are already taking place. In the 3-population wound, perpetual complexity arises in the logistics of: injury & thrombosis -vs- acute inflammation -vs- wound module -vs- chronic inflammation -vs- injury & thrombosis –etc.-etc.-etc.

At this point, we can actually draw a closer parallel to the sheep-grass analogy, by looking at the dynamical symmetries in this mix. Normally, acute inflammation (ai) has an inducing or proliferative effect on the wound module (wm), ai gÉ wm. In a normal wound, that is all there is to it, acute inflammation turns on healing, and each phase runs its own course. (Normal healing does not have direct inhibitory feedback on inflammation. Instead, inflammation runs its course, and if there is no further injury, then it extinguishes itself as repair ramps up. To the extent though that repair keeps the tissues in a “good state” that inflammation is not alerted to, then the wound module can be seen as having some inhibitory feedback on acute inflammation, ai Vf wm.) In the chronic pathological wound, chronic inflammation (ci) joins the mix. Chronic inflammation has an effect to suppress or upset the wound module, disorganizing it or retarding its kinetics, ci gV wm. The altered wound module in turn is creating auto-sensitizers and exposed antigens which fuel the chronic inflammation ci Éf wm. Note the symmetries in these dynamics: acute inflammation begets wound module; chronic inflammation suppresses wound module; normal wound module suppresses acute inflammation; altered wound module promotes chronic inflammation. Thus, we have a system of mutual feedback, mutual promotion and inhibition, mutual predation and deprivation, mutual induction and suppression. These are precisely the types of dynamics that affect the simple grass-sheep system.

There is a reason that chronic and pathological wounds act “locked in”, now a bit better, now a bit worse, but fundamentally unaltered over long periods. They are locked into a dynamical attractor where acute inflammation, an altered wound module, and chronic-immune-lymphocytic inflammation compete and promote and can not easily escape. These dynamics are easily understandable via the principles of non-linear population logistics.

When healthy (the 2-population wound), recurrent primary injury and thrombosis are needed to perpetuate the wound and the wound control loop.

When intrinsic chronicity occurs (the 3-population wound), the system is locked into a persistent chaotic attractor without needing new inputs.

26

This slide emphasizes the last few comments from the preceding slide.

When the wound is intrinsically healthy, with the normal and expected 2-populations of acute inflammation and wound module, then recurrent primary injury and thrombosis are needed to perpetuate the wound and the wound control loop. When intrinsic chronicity occurs, chronic inflammation creates the 3-population wound, and the system is locked into a persistent chaotic attractor without needing new inputs.

Perpetual complexity arises in the logistics of: injury & thrombosis -vs- acute inflammation -vs- wound module -vs- chronic inflammation -vs- injury & thrombosis. These inter-mixed and inter-dependent populations have abnormal dependencies and feedbacks leading to multicontrol and n-body dynamics, loss of sigmoidal one-shot behavior, and chaos and non-converging attractors. As problematic as this might be from a clinical point of view, this system can enter an attractor that is dynamically and thermodynamically stable, a low energy well that it cannot so easily escape.

On the left panel, the wound control loop is shown, with extrinsic injury and thrombosis summed in (i.e. primary disease – trauma, allergy, immunity, hypercoagulability, etc). Obviously, if the loop was otherwise running as a one-shot, winding down as the wound healed, then these added events would simply expand the wound, cause more inflammation, and elevate the whole system to an earlier more active phase. On the right, chronic inflammation has been added in with the other major dynamical compartments (injury & thrombosis, acute inflammation, wound module). This adds a variety of new dependencies, both promotional and inhibitory, which complexify the patterns of feedback and thereby lead to chaotic behaviors.

27

The top picture shows a young wound, still open, going through the process of active proliferative wound healing. This is a healthy wound. The architecture of the wound module is present, but in any given area, the structures are largely amorphous or loosely organized. In the bottom picture, an old scar has remodeled itself back to nearly normal fascia. The arrangement of angiocytes and fibroblasts, vessels and connective proteins, is very nicely ordered and periodic. There is no blueprint of how to do this, yet it happens dependably well in the healthy patient and wound. The Main Control Loop drives wound healing toward the system reference. How does it know what the reference is? How do wound module elements know to organize into the required form that satisfies the reference?

To study the physics of wound healing and wound pathology, we have so far looked at three foundational subjects in non-linear dynamics: (1) control, (2) chaos, attractors, n-body dynamics, (3) population logistics. The answer to the above question comes from a fourth subject in non-linear dynamics: cellular automata & self-organization.

28

The whole wound healing system represents another foundational concept in non-linear dynamics – it is a class of cellular automata. Self-organizing automata are systems in which individual elements, “cells”, have a set of strict deterministic rules governing their behavior and how they must interact and evolve with adjacent or local cells. If you throw them all into a pot, they will sort themselves out, generally ending up with complex highly organized structures based on just a few simple instructions or relationships.

Biological systems which are undergoing embryogenesis, growth, and repair are all self-organizing automata. Growth and repair have no architectural blueprints to follow. Cells and chemicals just do what they do, obeying basic physical, chemical, and biological principles (the deterministic “rules” of the system). In so doing, proper structure develops. Dynamical and thermodynamical principles of energy and conservation ensure that systems will passively and blindly “seek the path of least resistance”, undergoing reactions or transformations that tend to dissipate free energy and maximize entropy and thereby seek zones of energetic or dynamical stability. These thermodynamic principles of efficient assembly are epitomized in the term “parsimonious self-organization”. This principle states that automatically organizing systems will take the route to self–assembly that takes the least information or energy or effort.

Essentially all organized structures and patterns in nature qualify as self-organizing automata, not just biological systems. In other systems, “cells” are the functional or interactive units that constitutes the base scale of the system. They may be physical units, or they may be abstract partitions or tilings of a space or medium. The key premise of cellular automata is that the behavior of each cell is determined locally by its interactions with its neighbors. Some behavior or change in state is induced as a reaction to what the neighbor is doing. Systems can be defined to have “neurological” functions (orders are issued from a central command) or “endocrine” functions (status can be telegraphed over a distance). However, the reality is that an extraordinary number of systems in nature and biology are just local “cellular” interactions. In biological systems, the dynamical “cells” are likely to be real biological cells. In the wound, each cell type or population has its own genomic program and “rules of engagement” that specify how it is to react to other cells or environmental features, and likewise how it is to influence the others. These are the rules of the system, and they govern what type of structure occurs. The illustrated examples on this and the next slide should give a sense of what cellular automata are and how they operate.

Left top: these are two examples of abstract automata generated by computer. Each pixel in the image is assigned a random value, black or white. On each iteration, the state-value-color of the pixel is tested and altered based on a strict set of rules. The rules typically are something like “if three neighbors are black then become white, else no change”, or “if the guy to the right and the guy below are black then become black, else become white”. I cannot recall what rules I used to generate the these two outputs, but that is irrelevant. What happens is that as the system is iterated, beautifully organized patterns show up and then remain stable (no changes on subsequent iterations) – just like a point on the Mandelbrot set or logistics map when it enters a stable orbit or convergent value after so many iterations.

Left center: Diffusion limited aggregation (DLA) systems are a great example of a simple cellular system that models many real world structures. The assumption is that the central structure grows by the aggregation of new material, and that the arrival rate of new material from the peripheral environment is much slower than the aggregation rate onto the structure. The system is iterated by starting a “particle” at a boundary pixel, then letting it do a random walk until it hits the existing structure, which is where it then sticks. This concept is extremely simple to model digitally, and the left panel shows a computer generated output. On the right is a picture of manganese dendrites on a desert rock, a nice example of the kinds of natural structures that are formed by DLA dynamics.

Below: These are samples of the VT (Vascular neT) model of angiogenesis. This model recreates the biological rules of angiogenesis based on the diffusion of oxygen and angiogenic factors, and the sprouting of new vessels on threshold conditions based on cell-to-network distances. The four panels to the left show the generation of new vessels over four iterations as the host tissue grows (the four panels have been resized to a common display size). The two panels to the right match a VT output to a picture of real blood vessels. The model accurately recreates vascular morphology based on a few parsimonious rules applied locally by repetitive iteration – i.e. a typical non-linear cellular automaton based explicitly on the natural rules of the system. (See the Arimedica website for more information about the VT model and angiogenesis: “Developmental Angiogenesis and the Biophysics of Vascular Network Formation”, May, 2006. http://www.arimedica.com/content/arimedica_vt_(slides)_2006-0516.pdf)

29

Here are more examples of automatic self-assembly in biological systems. They are easy to find, because the body and its components have no means of organization other than cellular self-assembly, parsimoniously organized. Remember, genes encode proteins, either structural proteins or chemical process regulators (enzymes). There are no morphology genes, They do not male plans or drawings. It is in their inter-operations that complex organization and macro-structure occurs. Simple chemical and physical interactions establish the small sets of deterministic “instructions” which govern how cells interact with local neighbors. The self-assembly of tissues and organs then occurs automatically. Non-linearity, feedback, and control are implicit & explicit.

Left top: The visual cortex of the brain is organized into ocular dominance columns. The inputs from the right and left eyes are separated into interdigitated bands. How this separation occurs, and how these bands or “columns” develop is a cellular automaton based on just a few rules. Local competitive promotion and inhibition between populations is the crucial physics that governs the interaction. It is easy to model digitally by iterative non-linear implementations of the rules. On the left is a picture of real columns. The other two images are computer generated. (1) Carreira-Perpin MA et al. A computational model for the development of multiple maps in primary visual cortex. Cerebral Cortex, 2005, 15-8:1222-1233. (2) Miller KD et al. Ocular dominance column development: analysis and simulation. Science, 1989, 111:123-145.

Left second: Animal coat patterns occur as the result of the diffusion of local promoters and inhibitors. Chemical diffusion is the constitutive physics that governs the interactions. These patterns can be modeled easily on a plane by iterating reaction-diffusion equations that let neighboring pixels or cells decide if they turn or not to produce pigment. Murray JD. Mathematical Biology, 2nd edition, Springer, 1993.

Left third: The same reaction-diffusion equations can model the on-off pigment patterns that develop in mollusc shells. It is analogous to a printer in which the shell is a piece of paper. The pattern is printed one raster at a time, with each “character” being an automatic “cell” (and a biological cell as well) that responds to the effects of its neighbors. Meinhardt H. and Klingler M. A model for pattern formation on the shells of molluscs. J Theor Biol, 1987, 126:63-69.

Below: Here are more examples of how the VT model can recreate branched network structures. Remember, the VT model operates by testing local threshold conditions of the distance between each cell and the network, a good example of automatic “cellular” self-assembly. Left, bile ducts form under the same dynamics as vessels, and they have the same patterns. Middle, the gastrovascular cavity of a platyhelminth flatworm is easily modeled by VT, since it is the same structure as our own vessels, governed by the same genes (vegf), occurring in a species that phylogenetically has not yet separated the food accumulating gastric system from the distribution functions of the vascular system. Right, the re-creation of veins in a plant leaf.

Wound repair and the wound module are just another example of this kind of automatic self-assembly and parsimonious self-organization / self-re-organization. When allowed to function properly, stromal rebuilding is automatic and correct, without any blueprint or collective knowledge by the cells of what is being built.

30

The wound, i.e. the reparative events that mend the injured tissues, is simply a matter of the stroma reorganizing itself. It is a process of self-assembly by the few types of biological cells which constitute the system. The rules or interactions which govern the process are functions of the interactions between nearby cells. As such, the wound is a cellular self-organizing automatic system – a cellular automaton – made of real biological cells. Their deterministic interactions are epitomized in the Main Control Loop.

The photos are portraits of cells that participate in the healthy and the pathological wound. Each normal intrinsic cell - monocyte, angiocyte, fibroblast, keratinocyte - has an assigned job. If allowed to function properly, stromal rebuilding & wound closure are automatic and correct. When the wound or its cells are pathological, than self-organization is disturbed or fails, and wound healing is disrupted – because wound healing is nothing more than the self-organization of these cells. Problems happen when chronic inflammatory cells appear. They disturb the orderly function and organization of the other cells that are meant to be there, arresting or disrupting their intended organization.

The organization of the wound is an automatic event when all is healthy. Recall from the images on slide 27 that the goal of all of this organizing is to get to a stable form. Those forms (mature normal dermis and fascia) tend to be highly structured and periodic, more “crystalline” than amorphous or glassy. In parsimonious automata, they get to that form with minimum information or energy, and that is the beauty of these systems, that such dependable and consistent form arises from so few inputs or instructions. If you look at the top pair of examples on slide 28, the computational automata, the fields start as random white noise. As the system is iterated, they organize toward the forms shown, and once they reach the final output, it no longer changes. Once it reaches the form shown, each subsequent iteration produces exactly the same pattern – it has become totally stable. This is like the non-linear logistics equation that gets to a stable single value or orbit after a few iterations. It is like the Mandelbrot set that likewise converges to stable orbits after so many iterates. Do you see the common dynamics of these non-linear systems? When convergent, they will stabilize to a dependable extremely stable form just by following the simple rules. Even if the resulting morphology appears very complex, it is nonetheless structured from a very minimum set of rules and is ultra-orderly, and it is ultra-stable if the system was able to fully converge. Once a wound is fully re-organized back to final scar-stroma-dermis-fascia, once it is fully converged, it is stable. Angiocytes and fibroblasts, vessels and connective fibers are then settled into their final positions and forms that will remain essentially unaltered for the remainder of the host’s life. (Whatever remodeling subsequently takes place in the stroma is a long time-base or slow decay-rate event that is then part of normal basal biology, not part of the original automatic assembly of wound healing.)

When the wound is pathological and organization is disrupted, the system is still a group of cellular automata. The problem is that it cannot converge on the intended form. It remains in a loose state of quasi or unsettled organization, trying to organize but remaining mixed up, remaining glassy and amorphous rather than crystalline, fluid or flowable rather than solid, plastic rather than elastic. As “iterations” or time continue, the structure can keep reorganizing and re-morphing, with cells and structures appearing, disappearing, flowing, shifting, reshuffling. It will never be fully settled until adverse “chaoticizing” dynamics that elevate the orbit are controlled and the system is allowed to converge. The failure to converge or fully organize is simply a consequence of non-linear dynamics: an iterative or n-body or multi-population system getting stuck on an attractor that cannot converge or settle. For the wound, breaking it out of a high-orbit attractor means controlling applied perpetuators such as continued disease, injury, or thrombosis, or eliminating the intrinsic pathologies that develop due to abnormal populations and population dependencies.

Recall too that the wound is a closed loop control system. How does that relate to automata? It has been implied so far that these systems all function rigidly with strict algorithmic repeatability. That is certainly true for the computational automata shown on slide 28, but it is not true for biological systems. Biological systems such as the wound are highly deterministic, but they must interact with the world around themselves, and that world is going to throw a lot of unexpected stresses, perturbations, and random variability in their way. Without control, the final output (a morphological structure in the case of the wound) would have to be pre-programmed, aka “calibrated”, and the environmental factors would throw that calibration off. With good control, healthy cells will react properly to whatever unexpected or aberrant conditions are present. Determinism and control will prevail, and the structure or morphology will form correctly in spite of the environmental stresses. That is explicitly the value of closed loop control over strict linear open loop programmatic determinism, that errors and stresses can be absorbed, overlooked, corrected, and accommodated. Control makes self-assembling biological systems robust and error-tolerant, unless the system controllers are sick or else the stresses on the system are so severe as to overwhelm its inherent capacity to react and correct.

The “dysdynamia” we are talking about should be distinguished from conventional disease. From the clinical perspective, the non-healing wound is a “disease”, a morbid state that interferes with health or function. However, the intrinsically pathological wound is not a divergent wound, not ulcerating and getting worse. It just is not healing. In the chaotic wound, what is sick is just the collective interactions of otherwise healthy cells doing what they are programmed to do in response to local stimuli. What is disrupted is ONLY the aggregate organization and self-assembly. In the chronic chaotic intrinsically pathological wound, not one of the cells shown is intrinsically pathological. Each cell and cell type is intrinsically correct or healthy, trying to do what it is meant to do. If it is failing, it is because it is being besieged, restrained, or deprived by another of these cells. If it is abnormally overactive and thereby disrupting things, it is because something else is stimulating, up-regulating, or otherwise turning it on. None of these cells is sick. Just their collective interactions are altered. From a clinical point of view, the system as a whole is sick. From a physics point of view, this is just the expected dynamically and thermodynamically mandated behavior of complex multi-control systems.

Dysdynamia of the system is the intrinsic disease of wound healing. Would it not be correct though to say that genetic or metabolic diseases of angiocytes or fibroblasts are themselves intrinsic diseases of this system? Yes, in principle. In actuality though, there are few if any such diseases. That may sound strange, given the spectrum and nature of other diseases that afflict the human condition. Nonetheless, there are few intrinsic disorders of the stroma and wound repair cells. For an explanation, see the addendum after slide 34.

31

At the start of this series (Part 1, slide 2) we saw examples of wounds that had no net change over long periods. Convergent wounds which are healing are the clinically desirable state. At the opposite end of the spectrum is the divergent sick actively pathological wound. While this is the clinically adverse state, it is dynamically easy to understand, and the principles of treatment to control disease and active ulceration are usually easy to implement. In between are the non-convergent chaotic wounds, the source of prolonged frustration, even exasperation. These wounds refuse to heal or even make progress, in spite of numerous reasonable treatments, even when gross pathology & causative disease are controlled and acute ulceration and inflammation are subsided.

We stated at the beginning that there is a reason: that these wounds go back and forth but get no better; that they cannot spontaneously climb out of this attractor; that multiple therapeutics are often of no benefit; that adverse behavior is independent of the primary pathology. Furthermore, these reasons cannot be understood: by looking at any individual cell or chemical or gene; by analysis of any dependent-vs-independent experiment; by any “conventional bioscience” type of experiment; by any type of randomized controlled trial.

We are now in a position to understand why this is all so. Wound failure is not the result of a gene mutated, and it is not the result of a chemical or metabolic imbalance. It is not the result of chronic degenerative changes in a specific organ or tissue, nor the result of obstruction, perforation, or other anatomical disruption. It is the result of a bunch of cells not being able to properly inter-operate and self-organize. The science required to understand this is not biochemistry and cell biology, not genomics and proteomics, not classical anatomy and physiology. True, these disciplines apply to understanding individual components of the wound, but the science required to understand how wound elements inter-operate and organize is physics. Specifically, the applicable physics for wound healing is non-linear dynamics. So far, we have looked at this subject from the point of view of several major aspects: control, chaos, populations, and automata. These aspects will now be brought together for an integrated view of the physics of wound healing and wound failure.

32

In our study of non-linear dynamics and the wound, we began by showing that normal wound healing is a regulated process, a feedback controlled loop that senses the state of the wound and can drive the wound healing machinery to restore an intact epithelialized stroma. When the control loop operates without perturbation or repetitive re-injury, then the healing of incidental injuries and wounds is a one-shot response, with reactive then reparative components ramping up then decaying as they complete their appointed tasks. In fact, each major block or component of the process – thrombosis, acute inflammation, wound module and repair – has a similar one-shot profile, each triggering the next into existence, each extinguishing after its task is accomplished.

Problems begin when some sort of primary injury or stressor on the system is sustained. There is a crucial physiological interaction between inflammation and thrombosis, each causing the other, and each able to be triggered by various primary conditions of coagulopathy, immunopathy, angiopathy, panniculopathy. Necrosis and ulceration are caught in the middle of this complex set of interactions. Repetitive or persistent or primary pathology can trigger the thrombosis-inflammation loop into a sustained state. This condition feeds back into the major events of the primary sequence of wound reaction and repair. Once thrombosis and inflammation are sustained, the one-shot profiles of healthy response and repair are destroyed. There are now multiple events, populations, control blocks, whatever – multiple “bodies”, i.e. N-bodies – feeding back in a system of complex multi-control. Each element or component is responding exactly as programmed. In fact, if you were to look at small slices of the system, you would continue to see proper linear or exponential or sigmoidal responses to incidental changes over short time scales. The problem is that the aggregate whole has become disarrayed. The system remains deterministic, operating according to its rules, but the overall behavior is one of back-and-forth, never crossing the finish line, in patterns that defy representation by conventional geometry or algebra, i.e. chaos. Once the aggregate wound response-repair system is in a chaotic state, the tail end of wound module and repair cannot run its course and succeed at its own business, which is the reorganization and self-assembly of the stroma.

33

Once we understand that the wound is a feedback regulated control system, that lays the foundations for understanding that chaotic dynamics can occur. Those chaotic dynamics are realized when abnormal perturbations, external forces, retriggers, and continued disease and injury keep boosting the system components into sustained states or activities such that one-shot dynamics and settling are preempted or disorganized. The problem is especially disorganized when multiple elements with multiple interactions (n-bodies) participate in the chaos. If all we talk about is chaotic systems in the abstract, that suffices to explain wound failure. However, these principles become more tangible when we start to address the physical reality of the wound, a set of self-organizing cell populations. The interactions of these cell populations under healthy circumstances is the basis for normal one-shot responses, based on the principles of Verhulst sigmoidal population logistics. One of the well founded principles of linear dynamics is that when constraints and feedbacks are placed on mutually contingent populations, chaotic dynamics occur. These populations are represented on the Main Wound Control Loop. The summation-comparator-detector node, the inflammation error signal, and the macrophage controllers represent the acute inflammation population. The mesenchymal controlled load and their output represent the wound module population.

Why does the CAP wound get into a state of unhealed dynamical stability, even one that is counter-productive to health? When the control loop runs without perturbation or retriggers, when its populations interact without abnormal dependencies such as predation or deprivation, then the loop runs clockwise with smooth Verhulst style one-shot dynamics. Under those healthy circumstances, it runs toward one attractor, the convergent healed wound. When various perturbations or sustainers challenge the system, then it runs counterclockwise as well, forward and backward at various times and segments, with abnormal interconnects, bypasses, short circuits, and feedbacks that sustain the operations of the loop. It cannot enter the stable convergent attractor of normal healing. If primary disease or injury is sufficiently active or strong, then it might enter the divergent attractor of active ulceration. That state is clinically undesirable, but it is an attractor, a locus of thermodynamic (and therefore dynamical) stability. If it cannot enter the convergent attractor, and if it is not on the divergent attractor, then the system can settle on its third attractor, a state of sustained non-convergent chaos. As an attractor, this too is a dynamically stable place for the system to be. (The system, the wound, can enter phases of higher free energy and intermediate status between attractors. These are the transitions from one state to another, the induction of active disease, or the induction of wound healing, transitions which occur when new energy or information is put into the system, such as an infection, a flare-up of primary autoimmune inflammation, a vascular thrombosis that restricts circulation, versus debridement of the wound or treatment with anti-immune drugs or procedural revascularization.)

It is under the conditions of sustained disease or injury that abnormal population dependencies develop. As presented in Part 2, sustained primary disease, inflammation, immunity, thrombosis, allergy, etc. can all lead to abnormal population admixture in both time and space. Once acute inflammation and wound module get a prolonged look and handshake with each other, then abnormal dependencies develop which can keep the control loop running in abnormal directions or cycles. However, the whole system is robust enough that if primary disease and injury are fully abated and wound conditions restored to reasonable anatomy and timewise or spatial organization, then Verhulst sigmoidal one-shot dynamics can be restored, and the system can again enter its convergent attractor. This is what we are doing with our basic wound therapies, to keep primary disease and injury under control, and to keep the main two populations separated, thereby allowing the loop to run smoothly in a clockwise direction, which is often sufficient to allow the wound to heal.

The problem gets even worse when a third population appears, chronic inflammation. This takes the place of sustained primary injury, and becomes the key element that perpetuates the intrinsic or self-sustaining chaotic dynamics of the loop. More on this on the next panel.

In the first paragraph of the previous slide, we talked about “ . . . components ramping up then decaying as they complete their appointed tasks . . . “ This was a bit erroneous because the cells and populations do not really have appointed tasks. Those are teleological attributes that we ascribe to them. The reality is that they just function according to the basic principles of cell biology – genomics, proteomics, ligand-receptor interactions, cytokines and signaling, mobility and secretory responses, etc. They just do their own thing – they just function. The aggregate correct responses occur, and the correct structures form, because they are self-organizing automata. Their few rules of interaction allowed to operate without interference result in parsimoniously correct morphology. That is the sole purpose of the wound module repair population, to organize into a specific anatomical structure. When normal dynamics are upset or obstructed, then that self-organization cannot be achieved, and the final intended structure, a reorganized stroma and healed wound, fails to form. That is how the control loop “knows” what the system reference is. It doesn’t need to know. As the correct structures form, passively-parsimoniously-automatically, then variances from normal get smaller, and the reactive response of inflammation is mitigated because there is less stimulus to turn inflammation on. The system reference is just a well of thermodynamic stability and minimum free energy that occurs as the system elements, the “cellular” automata of self-organization, find their basal state of assembly.

One of the crucial issues to keep in mind about the failing non-healing wound is that the cells and cell populations are normal, acting and reacting as expected according to their genetic program. In the chronic chaotic non-healing wound, whether extrinsically (2-population) or intrinsically (3-population) pathological, not one of the cells is itself intrinsically pathological. Remember, these are not divergent wounds - not ulcerating and getting worse. They just are not healing. What is disrupted is only their aggregate organization and self-assembly. In fact, in comparison to other cells and organs, wound cells and populations have remarkably few intrinsic diseases or genetic defects. They remain inherently healthy and functionally correct through thick-and-thin, “failing” only when they are responding normally and correctly to disordered inputs or environment. This point is discussed further in the addendum after the next slide.

The wound is a system and its aggregate behavior must be studied that way. However, the individual elements in the system are tangible physical and chemical and biological items which must obey all rules and principles of physics, chemistry, and biology. The interactions, dependencies, failures, and assembly of these various elements are based on specific genes and chemicals and cell responses, the stuff that conventional bioscience research has been able to elucidate and characterize for bazillions of individual cell structures and biochemicals. These are the nuts and bolts, the wires and components, glue and nails, the grease and gasoline that keep the wound healing machinery moving and building. System physics and non-linear dynamics explain how they interact in time, and how their aggregate behavior succeeds or fails, but it is still necessary to understand how these broad events are implemented or actuated by tangible physical components. These nuts-and-bolts items and interactions must equally be known for an understanding of wound failure to be complete. How it is that specific wound healing cells, chemicals, and interactions are degraded, disorganized, deprived, & denied are a matter for conventional biosciences to continue discovering.

This brings us back to our primary points. (1) When the wound, host, and system are intrinsically healthy, then recurrent primary injury & thrombosis are needed to perpetuate the wound control loop. (2) When intrinsic chronicity occurs, the wound system is locked into a persistent self-sustaining chaotic attractor without needing new inputs . . .

34

This series of papers is meant to elucidate what the intrinsic disorders of wound healing are. As presented in the addendum below, wound healing cells, angiocytes and fibroblasts, are robust, well-tested, and largely error free, with extremely few genetic errors or primary diseases. When the wound system goes wrong, it is because these healthy cells get confused about how to interact and assemble because they are getting barraged by abnormal inputs. The abnormal inputs may be extrinsic to the core dynamics of the wound, or they may come from within.

Acute wounds. First, consider the normal healthy wound. This is due to incidental or one-time injury – a cut or scrape, a burn, a surgical incision, a myocardial infarction. The entire wound response and repair system is then triggered into existence. If there is no further injury, then there is a smooth uprise and then decay in the logistics and dynamics of the response. The uprise in the acute inflammation and repair populations, from zero to peak, follows sigmoidal (linear) Verhulst dynamics. These populations then decay as their controlled tasks complete. The coordinated behavior of these populations is a series of sequential one-shots. The result is a parsimoniously reassembled stroma with epithelial sequestration, i.e. normal wound healing. Problems happen when something sustains the system, some set of repetitive or persistent injuries or disease that keep re-initiating or amplifying these processes.

Chronic wounds – extrinsic (2-population chaos). Wound chronicity begins with persistence of disease or injury. This could be the prolonged action of untreated disease (inflammatory, thrombotic, immune, allergy, traumatic, etc), or it could be disease or injury that intermittently relapses in spite of treatment. This even includes a wound that may no longer be subject to the original event, but which is in a sustained state of acute inflammation due to neglected or improper care, i.e. the “uncontrolled wound”. The dynamics of extrinsic chronicity reflect several possible states. First, the wound may not be chaotic, but rather divergent, i.e. actively sick and ulcerating due to the effects of sustained injury or disease. Alternately, it may be on the convergent attractor, actually healing, but doing so slowly with only minute changes during short intervals of observation. These scenarios are akin to those regions on the Mandelbrot set where the system is near the chaotic boundary, and thus takes a long time to arrive at the definitive states of divergence or convergence. The key point though is that extrinsic chronicity reflects a state of 2-population chaos. As we know from basic principles of non-linear population logistics, even two contingent populations can have chaotic dynamics, sustaining and promoting each other while concurrently suppressing, depriving, or predating each other. The two populations here are acute inflammation and wound module. In the normal one-shot acute wound, these two populations stay separated by time and space. Their admixture and abnormal dependencies develop only as a consequence of sustained primary disease or injury.

When the wound, host, and repair system are intrinsically healthy, then recurrent primary injury-disease-thrombosis-etc are needed to perpetuate the wound control loop. The inverse is true too, that if primary stressors or promoters are abated, then the control loop is not perpetuated and it can settle. This means that clinically, CAP wounds due to extrinsic correctible causes are generally easy to heal. They are suppressed or subverted by acute inflammation, but acute inflammation abates after primary disease and injury and other sustained stressors are relieved. This of course is what happens in wound practice day in and day out. Basic hygiene and topical care are initiated, inflammation and edema are relieved, then causative diseases and risks are corrected. Once these basic milestones are achieved, the inhibitory population of acute inflammation can no longer suppress or attack the repair population. Once relieved, wound dynamics settle back to one-shot profiles, chaos disappears, and normal repair dynamics pick up again. The problematic difficult-to-heal wound occur when intrinsic 3-population chronicity ensues.

Chronic wounds – intrinsic (3-population chaos). Intrinsic chronicity occurs in association with the appearance of a third population – chronic inflammation. With extrinsic chronicity, outside forces need to be active to sustain abnormal behavior. When intrinsic wound chronicity occurs, the system gets locked into a persistent attractor without needing new inputs. Primary external diseases and injury can be removed, yet chaotic and sometimes even divergent dynamics will persist. Once the wound becomes autonomous and self-perpetuating, it is no longer easy to heal, because the inhibitions and negative dependencies of the third population cannot be so easily removed or reverted. As all wound clinicians know, these wounds are in fact exasperatingly difficult to heal.

As for the extrinsic wound, problems begin with sustained primary disease or injury. Underlying primary inducing disorders are those of chronic inflammation (reactive & induced), infection-immunity, trauma-injury, allergy-atopy, and thrombosis & micro-occlusion. With prolonged admixture of acute inflammatory cells, transformed inflammatory cells (macrophage-histiocytes), early incidental lymphoid cells, and repair cells and products, the risk is that sooner or later auto-immunization will occur against repair cells (angiocytes and fibroblasts). The third population of chronic inflammation appears. Since it is explicitly tied to the repair population, these two populations cannot be so easily separated, making the third population intrinsic within the wound. This third population brings with it predatory dependencies and suppressions which subvert the functions of the repair population. Without specific intervention or treatment to correct this situation, that’s that, and repair is fundamentally put out of commission.

It is quite interesting to read extant literature on the subject of peri-vascular lymphoid infiltrates. It is seen with all of the pathological associations that we might expect after taking a look at this subject from a wound and immunopathy point of view. Nonetheless it is not recognized for what it is, nor its association with wounds and impaired healing, even though the nature of lymphoid cells are well understood. Here are a few quotes / paraphrases from relatively recent journal articles:

“ women 20-34 years - infiltration of vessel wall by mononuclear cells, mainly lymphocytes - 4 patients antiphospholipid antibodies - one heterozygous factor V Leiden - we term this lymphocytic thrombophilic arteritis “

Lee JS, Kossard S, McGrath MA. Arch Dermatol. 2008;144(9):1175-1182.

“ criteria for lymphocytic vasculitis (1) lymphocytic infiltrate blood vessel, (2) fibrinoid necrosis, (3) endothelial cell hyperplasia - clinical diagnoses varied - drug reaction, chronic urticaria, nodular scabies, erythema multiforme, - probably not specific - more likely a reactive process “

Massa MC. Journal of Cutaneous Pathology, 2006, 11(2): 132–139.

“ lymphocytic vasculitis as sign of early connective tissue disease - hemorrhagic acral livedo with anti-ribonucleo-protein antibodies - striking lymphocytic vascular reaction - , perivascular extravasation of red cells, leukocytoclastic debris - finally developed systemic lupus erythematosus “

Oh CW, Lee SH, Heo EP. Am J Dermatopathol. 2003 Oct;25(5):423-7.

“ lymphocytic vasculitis - correlates with broad clinical differential diagnosis - connective tissue disease (mostly sle), rickettsia and viruses, idiopathic lichenoid dermatoses, perniosis, ulcerative necrotic mucha-habermann “

Carlson JA, Chen KR. Am J Dermatopathol. 2007 Feb;29(1):32-43.

Pathology textbooks have varying amounts of information on the subject of lymphocytic vasculitis. One of the more thorough discussions is in the large dermatopathology textbook Skin Pathology (Weedon D. 2^nd edition 2002 Churchill Livingstone. pp 242-253, and nearby chapters). In all of these writings, the emphasis is on describing histological features and correlating them with eponymic clinical syndromes, a “dead poet’s society” of dermatology. There never seems to be an appreciation of underlying core pathophysiological principles and mechanisms. The problem is that wound healing is not recognized as a part of pathology, and wound pathologies have little or no recognition or appreciation among pathologists, dermatologists, and others who have written papers such as above (see Part 2, slide 59). One of the common mistakes behind this failed appreciation is that technical and vernacular meanings of the word “chronic” are often confused or ignored. Histologically, chronic inflammation appears as granular leukocytes (eosinophils, especially with allergic and atopic conditions) and as lymphoid cells (lymphocytes and plasma cells). There is a tendency for pathologists to issue wound reports that just say “inflammation” or “acute and chronic inflammation” or something along those lines, with no further comment (your experiences with your own colleagues in Pathology may vary . . . but I doubt it). Comments like this trivialize the identity and functions of the chronic inflammatory cell set. They mislead people into seeing chronic inflammation as just a long standing substitute for acute inflammation. “When inflammation starts, it is early, and therefore ipso facto it is acute . . . but when it hangs around long enough, then we can call it chronic because it has been there a long time.” See how technical and vernacular definitions are getting confused in that kind of implicit thinking? (Perhaps the term “chronic” should be ditched from the lexicon of inflammation, using instead “lymphoid inflammation” or “lymphoid infiltration” to eliminate any confusion or misinterpretation.) The reality is that chronic inflammation is entirely different than acute inflammation in terms of biological functions and implications.

All cells have specific parsimoniously defined biological functions. This includes “chronic inflammation” lymphoid cells, the 3rd population of the pathological wound. In other words, all cells have explicit functions. The reason that there is so much differentiation or “speciation” among the various cells, tissues, and organs of the body is that one cell can only do so much. Each cell has a major function, such as secreting mucus or making thyroid hormone or contracting when triggered by a nerve. Granted, many cells have a number of ancillary or collateral functions, but the differentiation and functions of a cell are still rather narrowly and efficiently defined. Lymphoid cells are the agents of immunity. They do not show up in the wound just because, not on a lark, not on a whim, not as a matter of confusion, not for a vacation nor a change of scenery, not in the rain and not on a train, and not in a box and not with a fox (with apologies to Theodor Geisel, Dr. Seuss). And, by all means, they are NOT the relief team. They do not get sent into the game because the first team is getting tired and needs a break. This isn’t a case of extra innings. Lymphoid cells have an immune function. If they show up in a wound, it is because some type of immune-related taxis, tropism, or induction is attracting, guiding, or maturing them there. They are attracted to angioid and fibrous elements of the stroma – that is what they hug once they are in the wound. This should not be surprising because that is what they get exposed to during prolonged admixed acute inflammation and auto-sensitization. Once they have this automatic attraction to stromal cells and structures, they are now part of the stroma and the wound. Their effects have become intrinsic in the wound, and they are presumably inhibitory effects.

In normal healthy acute wound healing, each cell – monocyte, angiocyte, fibroblast, keratinocyte – has an “assigned” job, a parsimoniously defined task. If they can all just do their jobs, then the wound self-organizes back to a stable stroma. When you look at a chronic and pathological wound, productive self-organization is not happening. However, from the point of view of a single plasma cell, monocyte, or fibroblast, there may be nothing really wrong, just “life in the ‘hood”. As automata, they have no insight or collective concept of what they are trying to build. Instead, as long as they are alive, they just do their own thing, day-by-day, reacting as programmed to local stimuli. And as long as local cells can indeed do their own thing, then the wound and stroma reorganize without problem. Problems happen when you throw a cadre of chronic inflammatory cells into the neighborhood. Are they good cops, bad cops, street thugs and bullies, misguided vigilantes, officially sanctioned law enforcement, civil defense, or sanitation workers to clean up the mess? It depends on your point of view, but if you are a neighborhood angiocyte, then that lymphocyte who doesn’t live on your street is probably going to beat you up. Although each cell is alive and functioning correctly, reacting properly to local events, the collective system and its set of cells fails to organize.

In acute and in extrinsic 2-population wounds, primary disease and injury sustain the wound. When acute inflammation can be eliminated, wound healing returns to normal. Once the third population and its dynamical dependencies and attractors have settled in, then they themselves sustain pathology. The third population is just another form of challenge or injury which can perpetuate problems. The difference though is that the third population is attracted to the repair population, and in so being it is intrinsic in the wound and cannot be eliminated by treating or relieving primary disease. Because of the third population’s intrinsic status within the wound, this becomes an inherently stable dynamical state that is hard to revert.

Addendum to Slide 34

Above, we mentioned that wound healing cells are robust, well-tested, and largely error free, with extremely few genetic errors or primary diseases. There are extraordinarily few native diseases of the stroma. Those that do occur are largely autoimmune in nature. We have seen in Part 2 why the connective tissue disorders are due to autoimmune states as opposed to some other general class of pathology. We have also established the connection between autoimmunity and the diseases of the general stroma. However, we have yet to answer the other side of that question: why are there no common diseases of the fascias, connective tissues, and general stroma related to metabolic alterations or genetic deficiencies? The full annotated answer is beyond the scope of this presentation, but a few basics can be explained.

The stromal cells, fibroblasts and angiocytes, represent evolutionary and phylogenetically ancient cells. Multicellular life appeared about 1 billion years ago, as single celled life learned that there is strength and survival advantage in cooperative association and the division and specialization of labor. There are two quintessential constructs needed to permit multicellular association and function: (1) some system for holding everything together in a stable functional anatomical form, and (2) some sort of distribution system to permit the interchange of nutrients, metabolites, and information. In animals, the system that evolved for holding things together is based on connective proteins, the most abundant of which is collagen. Collagen structures and anatomy became increasingly complex as life advanced, but collagen is present even in the most primitive of multicellular organisms, the Porifera, the sponges. Evidence of a bulk transport system – a vascular system – is also seen in some sponges, and it is permanently established by the Cnidaria, the hydras and jellyfish. Primitive invertebrates do not have a blood circulatory system. Instead, their gut has extensions into all parts of the organism to directly deliver food, a gastrovascular cavity that handles both digestion and distribution. Nonetheless, this is a vascular distribution network, and our blood circulatory vascular system is a direct evolutionary descendant of the gastrovascular cavities of the Cnidaria. Only one gene and its product are required to govern the formation and morphology of this vascular distribution system, and that gene is VEGF (vascular endothelial growth factor; well, actually 2 genes, VEGF and VEGFR, its receptor). Genetic sequencing allows us to recognize the specific nucleotide “spelling” of each gene, and jellyfish and human VEGF and VEGFR are highly homologous, spelled almost exactly the same. Also, the observable functions of VEGF on vascular cells and structures are identical for jellyfish and humans. As life evolved, many new genes appeared, old ones disappeared, and many morphed and changed. But, over eons of multicellular evolution, VEGF and its functions are unchanged. Why?

Why has VEGF remained unchanged? Because multicellular life is wholly contingent on a bulk transport vascular distribution system. Without it, complex multicellular life is categorically impossible. (Likewise for the proteinaceous support matrix that structurally binds organism together.) Once this core infrastructure element of life had been written, it needed no revision, because it worked so well. What this means is that for the few quintessential genes that permit multicellular life, there is little room for mutation. VEGF is so crucially essential for life that without it, an embryo unconditionally cannot develop – period - exclamation. (In some experiments, VEGF knockout is categorically lethal; in other experiments, other angiogenic factors can keep a conceptus alive, but with significant developmental defects.) Whatever VEGF mutation might occur in a gamete, it cannot be propagated, because a conceptus simply cannot develop beyond just a few cells (the gastrula stage). The basic stromal structure of multicellular life – connective matrix and vascular distribution system – was worked out from the beginning, 1 billion years ago. The formation and function of these structures and cells has been thoroughly tested and debugged, meaning they are essentially error free. These core infrastructure functions of multicellular life are so consistently conserved and dependable, so thoroughly robust, that there are no major genetic or metabolic disorders of the stroma, and consequently none of the mesenchymal component of wound healing. Because these cells and structures have extraordinarily few intrinsic disorders, when wound healing goes bad it reflects some sort of exogenous disorder or damage, some sort of deprivation or attack affecting these cells and structures. That includes non-specific non-targeted conditions such as trauma, ischemia, toxicities, and severe metabolic-nutritional inadequacy. It also includes targeted damage directed against these cells and structures, and as we have seen in this section, that means the auto-immune disorders.

35

These diagrams summarize the points of the last slide. On top is the Main Wound Control Loop. Some of the blocks have been corralled into two major groups, representing the two essential populations of wound healing, acute inflammation and wound module. In addition, exogenous injury is summed into the loop, as explained in Part 1. Obviously, ongoing primary injury will keep re-elevating the state of the wound, even as the control loop is otherwise trying to wind it down. This is the basis for 2-population extrinsic chronicity and chaos (which can also eventually spawn the third population).

Below right is the graph from slide 26 showing the dynamics that occur when chronic inflammation is added. Recall that in Part 1 it was stressed that the control loop is an open model that can represent all states of wound physiology and pathology. Below left, to keep consistent with the control model, chronic inflammation and the smaller graph are melded into the main loop. The chronic inflammation population has inhibitory effects on the wound module population, and promotional effects on the acute inflammation population, as well as promotional effects on the state of the ulcer. If ongoing acute injury or disease were also added, then that would be another layer of control, making the dynamics yet more chaotic. Notice that chronic inflammation occupies a similar position as active injury, and it serves the same dynamics of sustaining ulceration, acute inflammation, and the ongoing operations of the loop. The difference is that extrinsic disease and injury can almost always be abated, allowing the loop to settle into the desirable state of one-shot dynamics, loop activity decaying as the wound converges on its fulfilled state of closure. However, chronic auto-immunized inflammation becomes intrinsic within the wound or stroma, and it cannot be so easily abated. As such, it acts like a generator or pacer to sustain wound injury and acute inflammation, to suppress repair, and in so doing perpetuate ongoing chaotic non-convergent wound dynamics.

36

We have seen that there are several primary inducing disorders that can perpetuate acute inflammation (and thus the wound control loop), increase auto-antigenic load, and risk auto-immunization by lymphoid sensitization. These are all disorders of chronic, recurrent, persistent, sustained injury, inflammation, and thrombosis, including primary inflammation (reactive & induced), infection-immunity, trauma-injury, allergy-atopy, and thrombosis & micro-occlusion. This slide illustrates the effects of primary disease or injury to perpetuate acute inflammation and potentially induce a state of auto-immunized chronic inflammation.

Left: a leg ulcer from a patient with polyarteritis nodosa. This view is from below an area of acute active skin infarction and ulceration. Vessels throughout the area were infiltrated by acute neutrophilic inflammation. It is this state of persistent or repetitive acute inflammation which chews up cells and releases endocellular debris and antigens. While this particular specimen had few chronic inflammatory cells, this would seem to be the type of patient prone to stromal auto-immunization, and quite likely it occurred long ago and is the basis for repetitive acute inflammation. Right: This patient developed acute progressive ulceration of the ankle after biopsy of a small lesion. She had protein C deficiency and positive cryoglobulins, along with histologic findings of thrombosis and vascular necrosis. In a patient with a primary hypercoagulable disorder, it is sustained small vessel thrombosis which can create ongoing low level acute inflammation as well as cause angiocyte necrosis and the release of related cellular debris.

37

This is another example of the effects of unrelenting primary disease to induce sustained acute inflammation. These images are from an 31 year old woman with a primary hypercoagulable disorder and ankle ulcer, along with miscellaneous immunopathic symptoms. Laboratory evaluation confirmed low protein C and low APC resistance (likely the primary problems), a positive lupus anticoagulant (probably secondary due to induced auto-immunity) and low factor IX (indirect evidence of a thrombotic state, due to compensatory down-regulation of a prothrombotic element). The specimens are from the base and edge of the ulcer. Features that can be observed include: acute and chronic inflammation, acute and chronic thrombosis, vascular necrosis or fibrinoid degeneration, wound surface infarcts, vascular disruption and disorganization, dense peri-vascular plasma cell and lymphocyte infiltration, cellular debris and basophilia deeper than expected for healthy wounds, cellular debris and basophilia along angiogenic cords, scant or disorganized fibroplasia, and an admixture of acute inflammation. wound module, and chronic inflammatory cells at different levels or strata.

As seen in the gross picture, there is active inflammation and necrosis in spite of treatment, representing persistence of the pathological state. Histologically, the overall architecture of the wound module is relatively correct, but numerous features are altered from normality. In this case, the primary hypercoagulable state is responsible for the persistent state of active infarctive and inflammatory pathology, which will in turn inhibit and delay wound healing, as well as create the conditions for auto-immunization. Recognizing an auto-immune component of delayed or disrupted healing becomes easier only after non-immune acute events have been controlled. However, in this case, the active pathological state was not controlled by anticoagulants and topical care alone, and persistent auto-immune inflammation may have been the persistent promoter of continued micro-thrombosis. Untangling the interconnections of acute inflammation, chronic inflammation, thrombosis, and their effects on subsequent wound healing becomes difficult, because this whole interconnected mess IS the intrinsic disease of wound healing.

38

This and the next few slides show examples of the third population, chronic inflammation, in wounds due to one of the typical chronic inducing disorders. These images are from two patients with primary hypercoagulable disorders. These views near the edges of the ulcers both show a vascular locus, i.e. a zone of vessels and angioid tissue within a dermal or connective matrix. The vessels have chronic thrombi and reorganization. The specimen on the left shows migratory spindle shaped disorganization of the angiocytes consistent with a state of chronic inflammation and nominal “wound healing”, i.e. growth factor induced mesenchymal cell activities. In both specimens, the vascular locus is heavily infiltrated with chronic inflammatory cells (lymphocytes, plasma cells, eosinophils). The left specimen is infiltrated with almost pure lymphocytes. The right specimen is infiltrated with mostly all plasma cells and eosinophils. There are few neutrophils, and the surrounding collagen matrix shows normal fibroblasts without inflammatory changes (that would have been much different if the specimens came from directly within the ulcer). Why are these vessels in a state of chronic immunogenic inflammation?

39

These images are from a 55 year old woman with chronic ulcers of the abdomen. She had a long history of chronic recurrent ventral hernia with numerous failed operations, and chronic abscess around polymer mesh. The mesh was ultimately removed, and the remaining open wound eventually healed by progressive contraction and epithelialization. As the patient neared the end of complete closure, she suddenly developed inflammatory changes and ulceration in areas of regenerated epithelium that had been healed and seemingly healthy for many months. Some of these new ulcers stabilized and became persistent and non-healing, whereas others continued slow progressive enlargement. Histology shows a rich mix of acute inflammation, chronic inflammation and wound repair. Left: this specimen is at the margin of ulceration (epidermal edge just a few microns away to the left). There is angioid proliferation consistent with wound healing events, but the vascular locus is completely filled with lymphoid cells. The epidermis above is undergoing active lysis by neutrophil invasion. The assumption is that the lymphoid cells have triggered a new round of acute lytic inflammation. This is a paradigm of the inflammatory-lytic pattern of necrosis and ulceration. Right: migratory spindle-shaped angioid cells would at face value appear to be normal, migrating chemotropically in a gradient field of angiogenic factors near the surface of the wound. Yet they have attracted the attention of a bevy of plasma cells. Within that intermix zone, the normal vertical migratory pattern of the angiocytes has been disorganized.

40

These images are from a 53 year old woman with lupus since age 18. She had had multiple abdominal ventral hernias and failed repairs. The current specimen was from a recent incision or scar that spontaneously started to erode and re-ulcerate. Left: at the edge of the ulcer, in the zone of active lytic ulceration, is a coagulum that is overrun with an equal mix of acute inflammation, nuclear debris, lymphoid inflammation (plasma cells and lymphocytes), and repair cells. This lesion is actively ulcerating, so repair cell proliferation is futile, non-productive, non-constructive, but their presence indicates that these cells are all attempting to do their nominal job. Regardless of the histologic presence of angioid cells, the wound was actively ulcerating (divergent), far from being able to organize and heal. Right top: a reorganizing set of vessels in the vertical migration zone in the upper strata of the wound. Here too is a mix of chronic and acute inflammation and wound module proliferation. The chronic inflammatory cells have an affinity for the angioid cells. Right bottom: a vascular cluster deeper in the dermis, in which lympho-plasmacytic infiltration is very dense. This was typical of most of the vessels in the specimen.

41

The left and center images are from a 34 year old man who was quadriplegic following spine injury. He presented with literally thousands of individual ulcers on trunk and extremities ranging in size from 1-2 mm through many centimeters. The active phase of ulceration began with eosinophil rich skin bullae, so the working diagnosis is bullous pemphigoid. No lesions would heal with generic topical therapies. Healing began with systemic steroids, but was only partial. Rapid complete healing was induced with azathioprine, which more or less proves that the chronic inflammatory population was the culprit behind the wound failures. Left: a vertical view of the wound showing a largely normal gross architecture, but with excessive edema and/or aminoglycan. Near the bottom are dark basophilic infiltrates which are almost all plasma cells. Clinically, the wounds were not healing. Histologically, although repair cells are present, there is no fibroplasia and incomplete organization of the stromal elements. Center top: a non-specific area showing intense admixture of acute inflammation, nuclear debris, histiocytes-phagocytes, lymphocytes and plasmacytes, and angioid reparative cells. Center bottom: Acute and lymphoid inflammatory cells surrounding and infiltrated into a vessel. The vessel itself is highly disorganized, the angioid cells only marginally associated or interconnected, and obviously leaky as evidenced by the significant hemorrhage throughout the area. Right top, bottom: These images are from refractory leg ulcers in a 53 year old man with rheumatoid. The tissues are dense with plasma cells as well as acute inflammation, intermixed with the angiocytes and fibroblasts of the developing (or not developing) stroma. Although the repair cells are present, they are failing to fully coalesce and stabilize. There is stasis and leukocyte trapping within the vessels. All three dynamical populations are here, acute inflammation, chronic inflammation, and wound module. They are admixed at multiple strata of the wound, and none of them appear as they should in a healthy wound.

42

These four images are from chronic and non-healing wounds in 4 different patients with various chronic antecedent injury or disease. They all show an admixture of acute inflammation and repair cells with chronic lymphocytic inflammation.

Left top: from a chronic sacral pressure ulcer. Pressure ulcers are due to a trauma. The cause of the wound is strictly extrinsic to the wound healing process, and such wounds are expected to have normal wound healing kinetics as long as pressure and other adverse mechanics and contact conditions are relieved. This is generally true, but there is also nothing unusual about a chronic pressure ulcer that seems to defy these expectations, acting impaired and difficult to heal even after topical conditions are completely relieved. These patients obviously have globally normal wound healing, and you can do surgery elsewhere on their bodies without problems, but the primary wounds seem to be misbehaved. The key element in this adverse transformation to an impaired wound may just be the state of chronicity itself, giving the wound a chance to develop some degree of lymphocyte-mediated auto-sensitization and disruption of the dynamical integrity of the wound module. This specimen is from the angio-attraction and angio-organization aminoglycan strata of the wound, and it would appear fairly normal except for one thing – the intense plasma cell infiltration along the vascular locus and elsewhere where angiocytes are streaming.

Left bottom: from a prolonged (years) ankle ulcer following radiation for a melanoma. With various treatments, this wound several times was nearly healed, but then re-ulcerated with no apparent provocation. Virtually every vessel in her specimens, whether under the ulcer or beyond its limits, had an intense wide lymphocyte infiltrate. On the wound surface (pictured), lymphocyte and acute inflammation are strongly mixed. Lymphocytes are especially intense around angioid structures (which elsewhere in the specimen are somewhat dysmorphic and disorganized).

Right top: from a patient with rheumatoid arthritis. This is another good example of the admixture of all three populations below the surface of a refractory chronic ulcer. Plasmacytes and lymphocytes are clustered in and around vessels and angiocytes.

Right bottom: from a 35 year old woman with a years-long refractory leg ulcer of uncertain primary diagnosis. Histology shows features of many CAP and immunopathic wounds: neutrophilic peri-arteritis (in a grossly bland uninflamed wound), plasma cell and eosinophil infiltrates, vascular disorganization, narrow or thin zones of aminoglycans and angio-organization, insignificant or disorganized fibroplasia, dense nuclear debris. In this specimen, the population admixture was intense, but also intensely disorganized. There were swarms of angioid cells, but not a lot of well-formed angiogenesis or coalesced vascular structures. In addition, there were an extraordinary number of angioid mitoses, present in most high power fields, sometimes 2 or 3, almost what you could expect to see with anaplastic cancers. These angioid cells were proliferating as they would in any healthy wound, but with bizarrely excessive turnover. Yet grossly the wound had only the scant appearance of “granulation tissue”, and it was largely absent histologically (failed organizational angiogenesis). One of those mitoses is seen here, in the midst of all the mayhem. If there was so much angioid turnover, yet no significant angiogenesis, what was happening? In cancers, new cells appear and accumulate. Here, they would seem to be rapidly generating then wholly disappearing. Possibly they were destroyed by acute inflammatory cells or else by immune mediated events. Perhaps they died by apoptosis, perhaps something else. Either way, they would leave behind a lot of potentially antigenic debris that could further the antigenic recognition and auto-sensitization against angioid cells and structures. The mitotic rate aside, the presence of chronic inflammatory cells, peri-vasculitis, altered behaviors of angioid and fibrous cells, and corruption of normal wound strata makes this a typical pathological wound, almost certainly of auto-immunopathic origin and intrinsic chronicity.

Addendum to Slide 42

We began Part 3 by asking what is the quintessential structure, function, and derangement of the wound. As we have seen, it is an ad hoc reserve organ made from a set of cell populations doing interactive things for the sake of reorganizing its own structure. Failure to organize is a derangement of the non-linear inter-operations of its normally controlled elements and constituent populations, i.e. a “dynamical disorder” or “dysdynamia”.

“Dynamical disorders” are getting attention from people who study a variety of complex systems in biology, because they affect cardiovascular functions, neurological functions, endocrine and nutritional functions, even population and herd dynamics, and everything else. As we saw in Part 2, it is the autoimmune connective tissue disorders (whether primary and a priori versus induced in the wound by chronicity and cell population admixture) that are the diseases which affect the intrinsic elements and individual components of the wound healing system. Dysdynamia is the disorder which affects their inter-operations and the collective function of the system.

In principle, recognizing the auto-immune or intrinsic chronicity component of delayed or disrupted healing becomes easier or diagnostically accurate only after injury, disease, and non-immune acute inflammation have been controlled. However, untangling the interconnections of thrombosis and acute inflammation, immunity and chronic inflammation, and their effects on wound healing becomes very difficult, because this whole entanglement IS the disease of wound healing. When the system gets entangled to the point that these core events in stromal biology cannot function properly and the wound module cannot converge, that is the intrinsic disease-disorder-pathology of the wound. Intrinsic wound chronicity is simply a non-convergent attractor of a chaotic entanglement of contingent cell populations. This attractor is clinically undesirable, the wound being seen as a refractory illness, but dynamically it is a stable state from which it cannot escape without deliberate treatment. Every therapeutic intervention that is tried is an attempt to unentangle the populations and dynamics of this multi-control system, trying to put “energy” in that can raise its orbit enough to shift to a more favorable convergent attractor.

Stromal autoimmunity, a targeted disorder of angiocytes and fibroblasts, is an essential inducer and maintainer of this intrinsic wound chronicity and dysdynamia. However, these are just two elements of a complex inter-operative system. What about all of the other things that might go wrong with the wound or its components, do they not also get sick and contribute to wound failure or wound incompetence? No, not much. In spite of the complexity of the wound, in spite of the bazillion individual micro-structures and chemicals that participate in the wound healing story, no, not much else goes intrinsically wrong with the wound. The reasons that there are so extremely few metabolic or genetic disorders of the stroma are for the evolutionary reasons discussed in the addendum to slide 34. However, the system has an Achilles heel.

When the wound module is left to itself, it very reliably self-organizes back to a stable re-epithelialized stroma. If there are no major genetic or metabolic disorders of the stroma, and consequently none of the mesenchymal component of wound healing, then when wound healing goes bad it reflects some sort of exogenous deprivation or attack. Under normal healthy circumstances, these extrinsic challenges come from the open ambient world. Normal wound anatomy is structured to provide its own protection. The plasma protein and inflammatory layer on the surface of the wound (with its host of neutrophils and related things) becomes the ambient interface, the protective barrier, a quite reasonable and effective substitute for missing epithelium. This top stratum provides perfect shelter for the repair process underneath. (See the Arimedica website for detailed information on normal wound histo-anatomy, especially the file arimedica_integra histogenesis_gottlieb-me_v2003.pdf). So, in principle, since the wound module elements are intrinsically error-free, and since they are protected from exogenous attack from above, then wound healing should work perfectly, and it does, except . . . Its Achilles heel is its unsuspecting soft underbelly. The only thing that can and does goes wrong is the unexpected auto-attack, a job from the inside. This is what happens when auto-immunization occurs and the defender system is directed against the repair system. This attack from a misdirected population is what disrupts self-organization.

43

Our focus has been on the auto-immunization of the stroma and the intrinsic dysfunction of the wound. Intrinsic dysfunction occurs when everything in the control loop is functioning correctly according to its own program, but elements are not cooperating or organizing due to population & dynamical chaos. It is important now to remind that not all chronic and pathological wounds are intrinsically impaired. Many are chronic (vernacular sense – there a long time), because primary disease or injury or other extrinsic causative factors remain active.

Here are examples where non-healing is due to identifiable extrinsic pathologies that directly injure or inhibit wound elements or disrupt control loop operations: an open tendon with open tendon sheath; a pressure ulcer with open inter-tarsal joints; an ulcer that starts and stops healing with cycles of hydroxyurea; a radiation wound; unnatural iatrogenic injury due to topical chemicals; an arterial ulcer over the tibia which healed promptly upon restoration of circulation and placement of a regenerative matrix (cadaveric dermis) so that repair cells would have a place to do their business.

These wounds are chronic and pathological, and the control loop and system dynamics remain active. The principles of chaos and dysdynamia apply. However, for extrinsically pathological wounds, the dysdynamia results from the sustained activity of injury and acute inflammation. This is the 2-population chronic wound, and they are generally easy to treat once primary disease and injury have been corrected.

It is the obligation of the clinician to make sure that diagnosis is correct so that proper treatment can be planned.

44

This slide is a reminder that this is a three part presentation that looks at wound pathology from the point of view of its applicable physics, elucidating the intrinsic dysfunctions of the wound as a result of dysdynamia, especially when stromal auto-immunization has occurred due to prolonged population admixture in a repetitively injured wound.

Part 1 – The Wound as a System and a Controlled Machine

Part 2 – Auto-Immunopathy and the Intrinsic Disease of Wound Healing

Part 3 – Chronicity and the Physics of Wound Failure

These presentations and supplementary materials are all available at www.arimedica.com .

45

SUMMARY

Chronicity, chronic inflammation, & the physics of wound failure

All systems – physical, biological, natural, engineered – must obey basic physical laws and relationships, e.g. thermodynamics, conservation, Newton, Ohm, Maxwell, physical chemistry, mathematics. The wound is no different. While conventional and classically trained bioscientists focus on biochemical constituents of cells and matrix and wounds, this approach to study cannot elucidate the inter-operational functions and failures of the wound. As a complex system, systems physics – aka non-linear dynamics – is required to understand the integrated timewise operations and failures of the wound.

The wound module is a special ad hoc reserve organ. It appears in response to injury, then vanishes when the wound is healed. As for any other organ or tissue, it has a core structure and function, a core mode of failure, and an applicable physics to explain its functions and failures.

What are the quintessential structures and functions of the wound? It is a collection of mutually interactive self-organizing cell populations. It has no other function than to organize itself into a generic stroma to support epithelium and other tissues.

What is the quintessential derangement of intrinsic wound pathology & chronicity? It is dynamical disorder of logistical self-re-organization among these populations. When it fails, it simply fails to organize to its intended final form, to complete its task to become something and then disappear.

What are the fundamental physics relevant to the wound? Non-linear dynamics, control, chaos, population logistics, cellular automata. It is the science of populations, their interactions, control, and self-organization. When it fails, it is a dynamical disorder of self-organizing populations.

46

SUMMARY

The Physics & Pathology of Wounds - 3

Chronicity and the Intrinsic Disease of Wound Healing

There are few inborn errors of wound healing.

What then is the intrinsic pathology of the wound?

It is a state of autonomy or self-perpetuation not contingent on the primary pathology.

It is a dynamical disorder of a complex system due to:

1 – Continued primary disease, injury, inflammation, thrombosis which leads to sustained acute inflammation. This is a predicate condition which leads to stromal auto-immunization.

2 – Stromal auto-immunization leads to the appearance of lymphocytic (aka “chronic”) inflammation. This becomes the abnormal 3rd cell population in the wound.

3 – Sustained acute inflammation (the 1st population) and chronic immune inflammation (the 3rd population) create population dependencies and feedbacks that continue to sustain thrombosis and inflammation and dynamical disorganization. They also create conditions of predation and deprivation that inhibit or disorganize the 2nd population, the repair module, thereby disrupting self-organization and keeping the wound from healing.

4 – A complex multicontrol system such as this mix will have certain dynamical behaviors or attractors: convergence (healing, the “healthy wound”), divergence (active disease and ulceration, the “sick wound”), or chaotic orbits (non-healing, the “impaired wound”). While the chaotic non-healing wound is clinically undesirable, it represents a dynamically stable attractor and thermodynamic basin that makes escape to a convergent attractor difficult to achieve.

Primary disease, injury, inflammation, thrombosis have a crucial role in perpetuating the early wound and in inducing chronic inflammation. Underlying primary inducing disorders are those of chronic inflammation (reactive & induced), infection-immunity, trauma-injury, allergy-atopy, and thrombosis & micro-occlusion.

Sustained primary disease and injury can lead to chaotic dynamics in the 2-population wound, To the extent that they continue, then the pathological non-healing state remains active and non-trivial to break. However, this state is generally easier to break than chaos in the intrinsic 3-population wound. In the extrinsic 2-population, if primary disease is controlled, which is almost always possible, then the repair module can function without inhibition, and organized wound healing resumes.

Once the third population and its dynamical dependencies and attractors have settled in, then primary pathology is no longer needed to sustain the problem. The wound can then persist even when good care has resolved acute stressors. Because the 3rd pathological population is inherently linked to the others, the pathology and dysdynamia become intrinsic, the 3-population wound. These are the wounds that are neither healing nor getting worse. They go through perpetual cellular and biological activity, but with no net gain. The inherent dynamical stability of this state resists treatment. This inherent stability makes such wounds clinically frustrating, but likewise they are safe and compatible with otherwise healthy life.

Stromal auto-immunopathy and 3-population chronicity are the intrinsic diseases of wound healing. The integrated timewise behavior of the intrinsically chronic wound must be understood via the physics of complex systems and populations – non-linear dynamics. The intrinsically impaired wound is a dynamical disorganization of its mutually contingent cell populations. Understanding the intrinsically chronic wound via its physics correlates readily with clinical behaviors and strategies for treatment.

In summary, when you look at an intrinsically pathological wound, chronic, difficult to heal, perpetually a bit better then a bit worse in spite of treatment, you are seeing the standard dynamics of a complex system as governed by the laws of the universe – physics. Dependencies between acute inflammation, wound module, and chronic inflammation keep the wound module from fully self-organizing. The linear dynamics of a one-shot perturbation and response to a single trauma in a healthy subject, i.e. normal wound healing does not exist in the chronic pathological wound. Instead, the chronic pathological wound exhibits typical non-linear dynamics, meaning chaos, orbits, and clinically undesirable but dynamically stable attractors that keep the wound module from getting to the finish line. They go through perpetual cellular and biological activity with no net gain. Wounds with intrinsic and auto-immunopathic chronicity are simply behaving as complex natural systems are expected to behave when their normal balance or attractor is stressed by added populations, promoters, or inhibitors. Such systems will tend to dwell in their attractors, for dynamical and thermodynamical reasons, and breaking the abnormal population entanglements and their chaotic orbits enough to get the wounds to heal requires deliberate “strong” therapies.

Epilogue

FINAL THOUGHTS.

The Physics and Pathology of Wounds has been a triptych presentation meant to present a thesis concerning the pathophysiology of the chronic and pathological wound. Several crucial points have been made covering a diversity of subjects. There are also a variety of loose ends and directions for further study.

In Part 1, The Wound as a System and a Controlled Machine, the main point was that the wound is a system, that no amount of conventional bioscience experimentation will elucidate the operational physiology of the wound, that systems must be studied as such using the relevant tools of physics and engineering, We started by showing that the wound, like nearly all healthy physiological systems, is a controlled system. Control makes sure that the wound healing system stays asleep until needed, then comes to life, builds a morphologically correct structure with just a few rules and cell types, then winds down and reenters standby mode once its job is complete. All of the components of the wound response and repair system have their place within the anatomical wound. They also have their place on a basic engineering control loop that has feedback and a way to correct variances from a reference state. The healthy wound and all states of pathology can be modeled on this loop. Dynamical behaviors, healthy and altered, can all be studied or understood from this perspective.

In Part 2, Auto-Immunopathy and the Intrinsic Disease of Wound Healing, we went from a physics and engineering perspective to a clinical and pathological perspective. “Rheumatoid” and other auto-immunopathic ulcers are a major class of chronic and pathological wounds, and they are difficult to heal. CAP wounds due to other diagnoses can also become refractory to care. The commonality is that the wound is just connective stroma (angiocytes and fibroblasts, vessels and connectives), wound healing is just the stroma reassembling itself, and autoimmune connective tissue disorders are diseases directed against the stroma. Whether patients have a primary or an a priori CVD-CTD versus their wounds having become auto-immunized and intrinsically chronic, it is just two similar pathways to the same common state. For at least some patients, such as those with primary hypercoagulable states, clinical CVD-CTD’s such as rheumatoid or lupus are the consequence of stromal auto-immunization from the sustained micro-thrombosis, making both the CVD-CTD and the wound healing problems sequelae of the primary pathology. The intrinsically chronic wound is just a phenotype or avatar or cultivar of the broad class of auto-immune connective tissue disorders. The induction of chronic lympho-plasmacytic infiltrates in the stroma correlates with chronicity and intractability in wounds that will not heal, and it should have a direct influence on treatments selected by the clinician.

In Part 3, Chronicity and the Intrinsic Disease of Wound Healing, the engineering aspects of the wound as a controlled process have been combined with the clinico-pathological aspects of intrinsic auto-immune wound chronicity to arrive at a physics based understanding of why the disordered anatomy and cell mix of the chronic wound makes it impaired and incompetent to heal. As a non-linear dynamical system subject to feedback and control, it will exhibit chaos, attractors, and n-body complexification. Overall, its dynamics fall to one of three standard non-linear dynamical states, convergence (healthy), divergence (sick), and orbiting or chaotic (impaired). The healthy wound has a separation of populations that ensures that each runs the control loop as a self-converging one-shot. Prolonged primary disease, injury, thrombosis, and inflammation create conditions of progressive 2-population admixture (acute inflammation and wound module) to the point that the immune system eventually “sees” and sensitizes to stromal auto-antigens. The subsequent induction and admixture of the “3rd population”, chronic lympho-plasmacytic inflammation, then locks the system into a self-sustaining chaotic orbit. Chronic inflammation becomes a “generator” within the wound to perpetuate the acute state and keep chaotic dynamics active, even after primary disease and injury have abated. These are the impaired intrinsically pathological wounds, neither healing nor getting worse. They go through perpetual cellular and biological activity with no net gain. The inherent dynamical stability of this state resists treatment. Getting them healed requires persistent treatment, with anti-inflammatory and anti-immune therapies topping the list of crucial specific interventions.

Part 4, A Gallery of Case Studies, was not given at the original presentation of these papers, but is presented here to illustrate concepts, patients and disease, and the direct utility of these concepts in making an accurate wound diagnosis and picking proper effective treatment.

If you are a classic bioscientist, it is likely that cell biology, biochemistry, genomics, and the like are your “cup of tea”. Perhaps you are asking yourself questions like “What are the specifics of how these cells interact with each other? How do they signal each other? How do they inhibit or promote each other? Does one cell directly suppress another, or does it ignore the cell and just block its excreted output? What chemicals and genes are on or off to implement these actions and reactions?” This third part of this series which explains the physics of wound pathology and wound failure may seem novel or tangential to these conventional “meat and potatoes” issues of biological research. However, the wound is a complex dynamical system, and complex systems MUST be looked at this way to understand their overall operations and failures. That is one of the great accomplishments of science in the past 40 years, that complex systems can in fact be studied and understood by non-linear dynamics, making this the “century of the system”. By focusing on the physics of the system, it is possible to see the dynamics and operational inter-dependencies that govern how wound cells will behave in the face of various normal and abnormal circumstances. In fact the physics of the pathological wound simply do not care much about how these biological interactions are effected, implemented, or actuated at a biochemical level. For example, growth factors are one of the main elements in the control loop, but that is because they are a control signal directly within the loop, However, their exact chemical structure is completely irrelevant to their system-integrated operational dynamics. The physics do not care if an angiocyte has a certain surface antigen nor if a fibroblast has a specific gene expression nor if an epithelial cell has such-and-such intracellular signaling pathway turned on – no more than it cares if the macrophages are wearing purple underpants. The physics of the wound is concerned with system level interactions, control, non-linearity and chaos, population interactions and logistics, thermodynamics and energy.

It is equally true though that the tangible biology of this system is equally important. It is vital to understand the nuts-and-bolts, brick-and-mortar, collagen-and-matrix alterations and failures that keep these populations from healing the wound – what gene, what protein, what signaler, what receptor, what cofactor or catalyst, etc. These are the issues of classical bioscience that must be answered for the picture to be validated and complete, and which must be answered in the biology laboratory. These are the discoveries or correlations which are most likely to lead to the development of useful new treatments. What is needed now is bioscience research to answer some of the concepts and questions presented here. The main questions to be investigated, based on the novel observations and theses presented here, are how it is that peri-stromal lymphocytes and plasmacytes exert their effect to retard or chaoticize the wound.

The nature and difficulties of “rheumatoid” wounds, their distinctive patterns of inflammatory-lytic ulceration, their correlation with auto-immune symptoms and endocellular auto-antibodies are all the stuff of everyday clinical practice in dealing with chronic and pathological wounds. When I started this study, and started looking very closely at the histo-pathology of these wounds, I had prior assumptions about what I thought I would see. I would see lymphocytes, plasma cells, and eosinophils, i.e. “chronic inflammation” – I knew that already - that is just basic non-discriminating casual freshman knowledge. What I also thought I would see would be signs of aggressive immune inflammation – antibody and complement fixation, killer T-cells, active lysis of angioid and fibrous cells, with non-leukocytic mesenchymal debris all over the place. Wrong. The lymphoid infiltrates are very clearly associated with the active wound, always within fractions of a millimeter up to a few millimeters from the wound surface or edges, but then tailing out. Lymphoid aggregates my be a bit deeper, but they are more isolated, more mature looking, and always isolated to the vessels or vascular locus. And that is another strong observation, that the lymphoid cells have a very clear affinity for repair cells, especially the angioid cells and their vascular structures. However, they seem to coexist peacefully enough. There are no signs of stromal cell killing. I have done immunohistochemistry on many of the samples seen here. There may be problems with the process and specimen handling (it is not a research lab), so I cannot validate what has been seen, but so far there has been little evidence of immunoglobulins or complement, even when the slide is overrun with plasma cells. Nonetheless, these infiltrates are (1) associated with wound chronicity and chaos, (2) they go away with treatment and then the wounds heal, and (3) they are associated with a number of impairments and disorganizational features in the wound histology.

When it comes down to the more tangible biology and chemistry of these events, how is that lymphoid cells mediate, actuate, orchestrate their effects on the wound or its components? What genes or biochemistry let them exert their adverse, suppressive, inhibitory, or disruptive dysdynamic effects? Are the lymphocytes even the chief mischief-makers or just markers correlated with a more sinister entity? Are they passive consequences of the problem, dragged secondarily into the melee, or are they primary culprits? If they are primary troublemakers, are their effects overt and audacious, or subtle and surreptitious? On slide 34 we said “. . . if you are a neighborhood angiocyte, then that lymphocyte who doesn’t live on your street is probably going to beat you up . . .” Perhaps that is true, but perhaps they are just pulling the tires off of your car so you cannot go anywhere, i.e. not so malicious, but equally effective. That is the key thing about understanding the dysdynamical physics of this system. These cell populations with their inhibitory dependencies do not have to be aggressive and offensive to make trouble. They just have to interfere or disrupt, and the system can just as likely get disorganized and get onto a go-nowhere chaotic attractor. It is quite possible, because one of the quintessential attributes of any chaotic non-linear system is that subtle little changes can have big dramatic effects. So, in coming up with potential explanations for what is happening, the following are features that are observed histologically, with some interpretations and hypotheses. You can see the examples in Part 4, a gallery of cases, posted on the Arimedica website.

Basic anatomical features.

Lymphocytes. In the wound, they look like typical lymphocytes, but in a variety of sizes as they are reacting to something and accumulating cytoplasm and nucleoplasm to do their immune functions or become B-cells.

Plasma cells. These are antibody producing B-cells. In the wound, they look like typical plasma cells. In the sickest most inflamed or refractory wounds, they can have a variety of morphological variations and multinucleate forms.

Eosinophils. Along with lymphocytes and plasmacytes, eosinophils are considered part of “chronic inflammation”. In the wound, they are typical eosinophils. However, eosinophils are generally markers of allergy. Their presence might be an incidental component of chronic inflammation, but it usually reflects some sort of primary allergic or atopic state. Drug reactions (due to oral medications or to wound topicals and dressing materials), atopic and eczematous dermatoses, and bullous pemphigoid are quite likely the original primary instigators of the whole situation (just like chronic thrombosis is for those patients with hypercoagulopathic states and ulcers). Lymphocytes and plasma cells mean immunity, and eosinophils mean allergy – two similar but different types of host defense. In the chronic wound, eosinophils generally represent an primary extrinsic stressor on the wound, whereas lymphocytes and plasma cells are due to the “intrinsification” of the process.

Lymphoid infiltration. “Lymphoid” means lymphocytes and plasma cells. In the lymphoid infiltrated wound, both cells will be found, sometimes almost pure lymphocytes, sometimes almost pure plasmacytes, and any mix in between. There is a clear predilection for angioid cells and structures, but organization gets looser and more admixed as you go higher (earlier) toward the wound surface. Although incidental lymphocytes and plasma cells might be seen now and then in young healthy wounds, they are distinctly NOT a part of normal wound healing, and dense infiltrates are pathological. Increasing density of the infiltrates seems to correlate with the chronicity and refractoriness of each individual wound – worse (harder to heal) wounds have more.

Lymphoid clustering and palisading. It is common to see these cells, especially plasma cells arranged in straight lines or compact clumps, but this just represents their alignment along vascular structures.

Lymphoid aggregates. Sometimes lymphoid cells, both lymphocytes and plasmacytes, but especially lymphocytes will arrange themselves in thick clusters, often appearing lamellated as they insinuate themselves between layers of angiocytes in a vessel. These will often persist in old scars or later in the process, even when things are healing and doing well. They appear to be chronic reservoir or standby structures. Remember that angiocytes NEVER divide preemptively, only in response to VEGF (or other angiogenic factors) under circumstances of need (growth and development, injury and wound healing, ischemia, tumors). Lymphoid hyperplasia and activity seems to be most disarrayed and dynamic in the midst of active wound healing and inflammation, when angioid cells are themselves their most migratory, mitotic, and metabolic. As angiogenesis subsides, mature lymphoid aggregates hug the mature vessels but seem to have no effect on them. This all suggests that the lymphocytes can recognize and stand by structures that they are sensitized to, but that they “see” their specific target and react only when angiocytes are “awake and walking”, when cytoplasm, nucleoplasm, and various cell products are exposed.

Germinal centers. Germinal centers (GC) are lymphoid structures where lymphocytes are becoming hypermutated antigen-specific B-cells, governed by large dendritic cells in the middle of the GC. I have not seen true germinal centers, but I have seen some lymphoid aggregates with large central histiocytic cells which might represent some sort of forme fruste or transition state. These have been in the most severely and chronically inflamed wounds. This supports the thesis that longer more aggressive more sustained acute inflammation is key to the advent of auto-immune recognition and sensitization.

Location of cells. Looking at the fine structure of the wound, lymphoid cells have a very strong affinity for angiocytes and vascular structures, everything from mature non-reactive normal vessels in uninflamed adipose fascias underneath to individual streaming angiocyte spindles at the top of the wound. They are occasionally aligned with collagen bundles and fibroblasts. Looking at the gross architecture of the wound, they seem to be never too far away from the action. Mature “reservoir” lymphoid aggregates may be seen in deeper uninflamed areas, but active infiltrates and clusters seem to be within microns to a few millimeters of the acute activity. It is common to see that if there is chronic scar at the base of the wound, with adipose under that, that the lymphoid infiltration will abate about half way down through the scar. Deeper infiltrates seem to have some loose association with primary CVD-CTD diagnoses as opposed to other primary diagnoses that subsequently become auto-immunized.

Lymphocytes in lymphatics. When infiltrates and aggregates are present, lymphocytes are often seen packed into lymphatics in the zone of all the action. It is unclear if these are blood borne lymphocytes that just prefer to then congregate and hang out in the lymphatics, or if lymphocytes are arriving at the wound via lymphatics. If the are arriving that way, then it implies that there is some sort of taxis or tropism flagging them down.

3-population mix. In the uppermost parts of the wound where acute inflammation is most intense and wound module is least organized, this is where the most intense and amorphous mixing occurs between the various cell populations. Admixture of equal amounts of acute inflammation, wound module, and chronic inflammation correlates with the sickest wounds, and is apt to be seen during active ulceration and divergence as well as in the most intransigent chaotic wounds. Admixture with necrotic stroma, nuclear and cytoplasmic and other basophilic debris, and with monocyte-macrophage-histiocytes is telling evidence of how auto-sensitization is occurring in the first place.

Pathological effects.

Destructive effects. As described above, there is little evidence of direct cell toxicities or killing by the lymphoid cells. This is especially obvious in older more mature peri-vascular aggregates away from acute zones and strata, where lymphoid cells and vessels seem to cooperate or at least tolerate just fine. It seems clear that the lymphoid cells have no negative interests or dependencies with regard to mature inactive angiocytes. When angiocytes get active, something is revealed to stimulate the lymphocytes or to attract their attention. Whatever it is, it is not directly lethal or destructive to the angiocytes or fibroblasts, and the repair cells and their structures seem to be architecturally mostly normal.

Non-destructive effects. Non-destructive effects occur in the form of altered architecture and anatomical disorganization of the wound. Cell population intermixture is increased, architecture of the newest vessels can be altered in various ways, (or not), new vascular density can be altered (too much or too few, usually too few), the plasma protein and aminoglycan strata can have abnormal thicknesses or ratios. The aminoglycan stratum (which is also the angioid vertical migration stratum) tends toward the thin side, a crucial defect, since without a place for angioid cells to develop into mature vessels, the rest of the process becomes retarded or arrested. Bizarre changes such as excessive angioid mitoses and presumably accelerated apoptosis are incidental interesting findings.

Matrix and aminoglycan effects. The weakness of the aminoglycan layer in some of these wounds might or might not have something to do with the lymphoid aggregates, and if so, then the next question is whether that is a direct effect of the lymphocytes versus an indirect effect via their effect on other cells. In the sense that these parameters are all present together in the impaired wound, they are all correlated, but what effect lymphoid cells have on the matrix can only be speculated. I have not yet done alcian blue stains to look at aminoglycans, but that might be instructive.

Effects on angioid cells versus vascular structures. It is easy to think of the immunization process as making antibodies which will fix complement and invoke killer T-cells which will then lyse cells and thereby destroy the tissue and create more ulcer. Perhaps that occurs sometimes during periods of active ulceration, but our focus here is on the impaired non-healing chaotic wound that is not actively ulcerating. The lymphoid cells are clearly not directly lethal to the stromal cells. Perhaps they would/should be to fungi and bacteria and whatnot, but our own cells are not getting lysed. It appears much more likely that lymphoid cells are responding to something that angioid cells make – some sort of integrin perhaps, some sort of matrix protein or glycoprotein that binds the vascular locus, some sort of cell surface receptor, protease, or other exocellular product that angiocytes might make. The lymphocytes and plasma cells are certainly getting more stirred up when wound healing is active and angioid cells are themselves active – transforming, mitosing, migrating, reassembling – doing all of those angiogenesis things that they normally do not do in the healthy reserve standby state. However, to the extent that key products or expressions of angioid function are affected, this seems to be enough to disorganize overall wound integration and self-assembly.

Effects on stroma materials versus cells. The same rationale applies to possible effects of the lymphoid cells on other chemicals or materials of the matrix as opposed to direct toxic effects on angiocytes and fibroblasts.

Neutrophil induction. When a wound is still actively ulcerating and size is enlarging, something is obviously killing epithelium as well as dissolving mesenchymal matrix. In biopsies from these lymphoid wounds where ulceration is still active, neutrophils are seen to be doing the acute damage. They are actively infiltrated across basement membrane into the epidermis, dissolving everything in their path. These destructive neutrophilic infiltrates are taking place just above non-destructive lymphoid infiltrates, and it seems that the lymphoid cells are instrumental in triggering acute inflammation. The hypothesis that the lymphoid chronic inflammatory cells are having an inhibitory effect on wound module cells remains correct in the physics-dynamical sense. However, biologically, the direct effect of the lymphoid cells might be on neutrophils which in turn inhibit the repair cells. The neutrophils might exert this influence in two ways. (1) As discussed in Part 1, acute inflammation has suppressive effects on repair processes, via a variety of chemical and cellular mechanisms, and neutrophils stir up acute inflammation. (2) Neutrophils are making destructive proteases that chew up the matrix. When neutrophil activity is intense, active ulceration occurs (divergent wound), but at lower levels of activity in the chaotic non-divergent wound, neutrophils may be continuously degrading the matrix or inhibiting repair cells just enough to ruin the ability of repair cells to assemble properly.

Non-immunoglobulin effects. The assumption on seeing plasma cells is that they are immune competent and making antibodies and thereby killing, defunctionalizing, or clearing cells. To the extent that plasma cells are indeed having a direct inhibitory effect on angioid and fibrous cells, the effect may be by some other unappreciated mechanism.

Direct versus indirect effects. To reiterate, from a dynamics point of view, lymphoid cells are having an inhibitory effect on repair cells. From a biology point of view, that effect might be direct or it might be indirect through intermediaries or other chains-of-effect or sub-loops in the system. The discussions of these last few items simply reinforce how important is the entanglement of acute inflammation, chronic inflammation, and repair cells, i.e. the 3-population wound, to inhibit repair by whatever mechanisms it does so.

Dynamical effects.

Reservoir functions and standby mode. As discussed above, the lymphoid cells seem to mature and go into a standby mode around vessels as the tissues mature or become free from inflammation. These residual chronic lymphoid aggregates may have no purpose whatsoever, or they might maintain some state of low level immune or other effects, or they might be memory cells waiting for some new event to re-activate them.

Local versus global effects. In looking at all of these specimens, from wounds of varying duration, severity, and refractoriness, from wounds with primary autoimmune disease, induced wound auto-immunopathy, and a variety of all other primary diagnoses, I have gotten the sense that lymphoid cells and their aggregates can either be bred locally and stay local, or they can become global in scope and effect. (1) The local variety of infiltrates seems to be in patients whose primary wound diagnosis is extrinsic, e.g. arterial disease or pressure or radiation. There is no generalized auto-immunopathy. The effects of chronicity and cell population admixture to create sensitized lymphocytes is a process that occurs “right there” and stays right there. The sensitized lymphocytes presumably are not taking themselves back to the “hive” to be memory cells in some faraway lymph node or germinal center. The infiltrates are always “within a stone’s throw” of the wound, representing local breeding of lymphocytes during acute phases, and those lymphocytes now they stay where they were born, even as the wound settles down and matures. (2) In patients who have an a priori CVD-CTD or other autoimmune disorder, and in patients who secondarily get widespread rheumatoid-lupus like symptoms due to the wound (e.g. hidradenitis patients), the auto-sensitization of lymphocytes against stroma, would seem to have a global effect. Whether there are memory cells or not, specific antibodies or not, whether they remain local or move on to central lymphoreticular organs are all obvious questions to be asked. This concept might help explain why some of the intense local lymphoid aggregates now and then have some features which look like they are trying to grow up and become germinal centers. These might in fact be reservoirs or depots for local memory cells which can cause persistence of the local wound healing problems even if the rest of the body is trouble free. This might explain for example why lupus patients often get local scar problems – cicatritis, panniculitis, or acute ulceration – when a remote inflammatory event occurs, such as a cold or pneumonia or urinary infection or trauma. Even other nominally healthy patients can have similar symptoms, such as women with silicone breast implants suddenly getting tenderness then capsular contracture after remote infections or injuries. In those circumstances, remote acute inflammation seems to be turning on local dormant immune cells which were bred during the initial injury and wound healing in that particular area.

Slow progressive auto-immunization. This is for me one of the most interesting observations and hypotheses. The most problematic intrinsically chronic wounds and the patients with the most active autoimmune diseases seem to have the greatest load of lymphoid cells in their wounds. However, chronic wounds of other origins, such as arterial, pressure, radiation, etc. also have lymphoid infiltrates. Keep in mind that when you look at benign healthy healing acute wounds, lymphoid infiltrates are uncommon. However, in our clinic we see patients with chronic problem wounds that are not healing, and that is where our biopsies are coming from. So, it is not surprising that even the simpler healthier wounds for the more trivial reasons have developed some features of chronicity in the interval before they started getting good care. At first I thought it peculiar and unexpected that pressure and arterial wounds were getting lymphoid infiltrates. However, there are two other observations about these wounds that are relevant. (1) These otherwise healthy non-autoimmune patients were also having “clean” wounds with no infiltrates in more acute areas. (2) The degree or load of the infiltrates seems to be related to the length or severity of the ulcer. Thus an arterial wound of only a few months duration might have just a few incidental scattered lymphoid patches, whereas a pressure ulcer of years duration might have quite a bit more, but still hardly anything compared to a lupus patient with active ulceration of a scar. The implication is that stromal auto-sensitization is occurring locally and that it is a random or stochastic or statistical function. In any given time interval, there is a probability S that an element of tissue within the chronic wound will become sensitized (S is basically the conversion rate, and it will reflect a variety of local and host factors, so it will be unique for each patient, wound, and set of circumstances). What is the lymphoid load L in the wound? First, we normalize the system by designating wound mass as 1, which means that we are now solving to find out what fraction of the wound has developed auto-sensitization and lymphoid infiltrates. There are now two ways to approach this. (1) We can assume that the load of lymphoid cells compared to the total mass of the wound is small, so the available space for sensitization to take place is always roughly 1. In that case, the change in L in a given interval is just the conversion rate S, so dL/dt = S, which solves to L = St, a linear zero-order (straight line) solution. i.e. lymphoid load is directly proportional to time. (2) Alternatively, if L will be a notable fraction of wound space, then sensitization can only take place in the remaining areas that are not yet sensitized. Thus, dL/dT = S(1-L), which solves to L = 1 – e^-St, which is logarithmic, rising asymptotically to 1. So, somewhere between a direct proportionality and a logarithmic curve, there is a time-dependent uprise in stromal sensitization in any chronic wound. It would seem that in otherwise healthy patients. this is the kind of sensitization that stays local. It does not imply any type of global auto-immunopathy, but it does explain why the more chronic (longstanding) a wound gets, the harder it is for some of them to heal because of the onset of lymphoid intrinsic chronicity (dynamical).

Other items.

Biochemical markers of chronicity. Wound research in the past 10 years has looked at wound chronicity from biochemical and other conventional bioscience points of view. There are important differences between acute and chronic wounds. Matrix proteases and cytokines & growth factors are two general classes of chemicals which have been studied closely, and genomic profiles through gene chip analysis have become a leading edge tool in the past 2 or 3 years. These studies all show substantial differences between healthy and chronic wounds. This would be expected. Acute and chronic wounds are two thoroughly different states. The findings of increased proteases and acute inflammatory cytokine profiles in chronic wounds is easy to understand when you realize that sustained acute inflammation is one of the necessary dependencies of this system, creating the conditions that lead to auto-sensitization, and being sustained by both the primary disease or injury and the intrinsically chaotic state of the wound. Different gene profiles are no surprise due to sustained disease and injury, sustentation of acute inflammation, over-activity of the control loop, and the appearance of a third population of cells. Acute versus chronic, converging versus chaotic, 2-population versus 3-population, Dr. Jekyll versus Mr. Hyde – these are two very different states, and something has to actuate those differences, i.e. genes, peptides, other chemicals. It would be very interesting to see explicitly how much of the variances can be attributed to lymphoid markers, which should be nearly zero in normal acute healing.

The causes of connective tissue disorders. For many years, researchers and clinicians have mused and hypothesized over the origins of rheumatoid arthritis, lupus, and the related collagen vascular and connective tissue disorders. Some have ascribed it to an occult pathogen because it happens in association with prior acute and chronic infections. Others have ascribed it to allergic or atopic states. Some to injury and sustained inflammation. One of the first “wow, that’s interesting” moments I had as medical student on clinical rotations was seeing a rheumatoid patient that had a list a mile long of allergies, to pharmaceuticals and natural allergens. That is common in these illnesses. It is easy to think that their rheumatoid causes multiple allergies, but most likely it is the other way around, a heightened state of allergy, atopy, and sustained acute inflammation eventually leads to stromal auto-sensitization. My first insights into this issue came from looking at patients, wounds, wound histology, and the laboratory profiles that we draw on our pathological wounds. It became clear after a while that when dealing with hypercoagulable and other micro-occlusive wounds, and also with “rheumatoid” auto-immune wounds, that sometimes the two classes of disease were easy to discriminate, but that often they were confusingly similar to each other, both the patient profiles and the wounds themselves. Careful history reveals features of both. Laboratory markers show unequivocal signs of both categories of disease, as shown in Part 2. When we frequently find Factor V Leiden in patients with crippling rheumatoid arthritis, that is no coincidence. It seems that perhaps as many as 85% of our patients with an apparent primary hypercoagulable state also have symptoms and laboratory markers of an auto-immune disorder. And as we have developed the thesis here, the chronic wound is a CVD-CTD in its own right. It was the wound histology that solidified the appreciation that auto-immune sensitization occurs as a result of the sustained diffuse micro-thrombosis. What it all means is that the lupus and rheumatoid class of autoimmune CVD-CTD, and other auto-immunopathies are all a result of some type of sustained primary disease and acute inflammation, including thrombosis-hypercoagulability, infection, allergy-atopy, chronic injury, etc., i.e. the items discussed at length in Part 2. What is key about looking at these wounds and their histology is that this thesis can be seen clearly, item by item, step by step. This thesis is an integrated explanation of the various reasons why auto-immunity occurs, accounting for the sciences and observations of inflammation, immunity, stromal biology, and the clinical and laboratory profiles of these pathological states and diagnoses. It is necessary now to do large correlative studies of one class of disease versus another to confirm these relationships, and to begin looking for the conventional bioscience laboratory markers of these events.

Arimedica.com. These papers are posted on the Arimedica website, freely available for appropriate educational, scientific, and clinical use. Part 4 of this series is a companion presentation with just case studies. It was not presented as part of the original series due to time constraints, but the case studies illustrate all of the points in this epilogue, as well as showing numerous clinical pictures of patients that have the problems discussed in the first 3 parts.

47

End

48

Abstract (as submitted in advance of the meeting)

The Physics and Pathology of Wounds. Part 3.

Chronicity and the Physics of Wound Failure.

Marc E. Gottlieb, MD, FACS Phoenix, AZ

The wound module is a transient set of interacting cells which collectively restore injured tissue to normality, a fibrous stroma of angiocytes and fibroblasts. Its healthy aggregate behavior is a well behaved machine, governed by the physics of control systems. A sick system can result from various extrinsic perturbations, but the core mechanism of self-sustaining persistent dysfunction, the true intrinsic disease of wound healing is chronicity itself, the paramount cause being wound module autoimmunization. This state is disruptive but not fully toxic or lethal, thus immunopathic wounds have complex behaviors, at times better-worse-stable-variable, often looking healthy, but always frustrating as they refuse to cross the finish line. How does one explain such variable behavior and the differences between normal and chronic-and-pathological (cap) wounds?

Simply stated, intrinsic wound pathology and chronicity is a dynamical disorder of complex populations. The physics governing complex behaviors in complex systems is non-linear dynamics (nld). In addition to control, three aspects of NLD are especially important to wound pathology. (1) Population logistics. Healthy healing is a sequence of one-shot self-completing linear events: primary injury & thrombosis –then– acute inflammation –then– wound module. Pathology creates abnormal population dependencies (nutrition, starvation, predation, cultivation) and a new population, chronic inflammation. Non-linear perpetual complexity arises in the logistics of injury & thrombosis –vs– acute inflammation –vs– wound module –vs– chronic inflammation –vs– injury & thrombosis. (2) Cellular automata & self-organization. The “cellular” agents of the wound module (real biological cells in this case) have a small set of deterministic rules of interaction with each other. When allowed to function properly, stromal rebuilding is automatic and correct. Under pathological conditions, self-organization, i.e. wound healing is disrupted. (3) Chaos & N-body dynamics. The net effect is that the wound, a set of several interacting cell populations, has 3 attractors (basins, dynamically stable states or behaviors): convergence (healing), divergence (ulcerating), and self-sustained chaotic orbits (chronicity).

Basic methods to demonstrate non-linear dynamics: left, the logistical map of competing populations; middle, diffusion-limited-aggregation, an example of self-organizing automata; right, attractors and chaos in the Mandelbrot set of complex-plane iteration. While seemingly abstract, these structures are directly correlated with wound events.

49

THE PHYSICS AND PATHOLOGY OF WOUNDS. PART 3.

CHRONICITY AND THE PHYSICS OF WOUND FAILURE.

Original presentation February 22 - 26, 2010, Maui, at the

The John A. Boswick, M.D. Burn and Wound Care Symposium 2010

The presentation and related materials are accessible at:

arimedica.com

Content may be used for non-commercial educational purposes.

Content may not be published or used for commercial purposes without prior license or permission.

Contact information is on the slide.

Copyright © 2009, Marc E. Gottlieb, MD

Revision 01a, February 22, 2010

50

These presentations and supplementary materials are all available at www.arimedica.com.

The Physics and Pathology of Wounds. Part 1.

The Wound as a System and a Controlled Machine.

Marc E. Gottlieb, MD, FACS Phoenix, AZ

The wound is a transient organ of inter-operating cells, triggered into being by injury and inflammation, then extinguishing as it completes its repair of injured stroma. It is a system. Conventional bioscience tends to characterize properties and interactions of individual or one-versus-another elements within a system, but physics is required to understand the integrated timewise behavior of whole systems. Intrinsic wound pathology and chronicity, and wound failure and therapeutics are easily explained when wounds are seen as a non-linear System (rather than as a collection of dual-element linear interactions). For normal wound physiology and for the pathophysiology of altered and failing wounds, the governing principles are the physics of complex systems: non-linear N-element dynamics, control science, population logistics, and self-organizing automata.

Understanding wound physics begins by characterizing normal wound physiology. The wound is a closed-loop reference-driven non-linear multicontrol system. Sick and altered wounds have layers of added complexity, but the quintessential intrinsic machinery of wound healing – the Wound Module of post-inflammatory wound repair – functions as just a single control loop. When tissues are injured, the Main Control Loop of physiological wound repair will drive cells to reorganize back to a repaired stroma.

The wound control system is composed of these elements: The system state is the open wound and its conditions. It is compared (?) to a reference, normal epithelialized tissue. Variances generate an error signal in the form of inflammation. This activates macrophages which are the system controller. They in turn generate a control signal in the form of cytokines. The controlled load is the group of local responder cells. Their output are the elements of histogenesis, which modify the state of the system, which then feeds back to the loop at the summing point. Any discussion or research of the collective behavior of a wound must acknowledge this basic control system.

51

These presentations and supplementary materials are all available at www.arimedica.com.

The Physics and Pathology of Wounds. Part 2.

Auto-Immunopathy and the Intrinsic Disease of Wound Healing.

Marc E. Gottlieb, MD, FACS Phoenix, AZ

Many chronic wounds result from disorders extrinsic to the healing process, e.g. pressure or arterial disease. What then are the intrinsic diseases of wound healing? Compare the wound to other organs. The quintessence of heart failure is that it is an inadequate pump, for lung failure it cannot exchange gases. But the wound is neither pump and pipes, nor bellows and diffusion membrane, nor is it like any organ with macro-anatomical structure. It is a transient collection of mutually interacting self-organizing cells. Stromal angiocytes and fibroblasts (wound cells) have remarkably few inherent metabolic or genetic faults. Dysfunction of the aggregate population is almost always the result of deprivation or predation. Adverse states can be caused by (1) non-targeted exogenous conditions such as arterial ischemia or repetitive trauma, and (2) targeted damage directed against these cells and their structures. As will be presented here, predation against the wound module is due to a state of auto-immunopathy in which lymphoid cells are sensitized to wound components. Not only does this occur with classic connective tissue disorders and other well-recognized auto-immunopathies, but it happens when a wound becomes intrinsically chronic and pathological. Hypercoagulability and other conditions of persistent thrombosis and acute inflammation are the underlying states that induce the auto-immunization. Simply put, intrinsic wound pathology and chronicity is a dynamical disorder of complex populations caused by auto-immunopathic disruption of the wound module.

In these chronic non-healing wound samples, the vascular locus is infiltrated with immune cells (left, plasma cells; middle, plasma cells and eosinophils; right, lymphocytes.) On the left, plasma cells are mixed with the migratory angiocytes (spindles) that are trying to assemble the wound. At middle and right, chronic thrombosis due to a primary hypercoagulable disorder is not only present, it is the root cause of this entire state.

52

These presentations and supplementary materials are all available at www.arimedica.com.

The Physics and Pathology of Wounds. Part 3.

Chronicity and the Physics of Wound Failure.

Marc E. Gottlieb, MD, FACS Phoenix, AZ

The wound module is a transient set of interacting cells which collectively restore injured tissue to normality, a fibrous stroma of angiocytes and fibroblasts. Its healthy aggregate behavior is a well behaved machine, governed by the physics of control systems. A sick system can result from various extrinsic perturbations, but the core mechanism of self-sustaining persistent dysfunction, the true intrinsic disease of wound healing is chronicity itself, the paramount cause being wound module autoimmunization. This state is disruptive but not fully toxic or lethal, thus immunopathic wounds have complex behaviors, at times better-worse-stable-variable, often looking healthy, but always frustrating as they refuse to cross the finish line. How does one explain such variable behavior and the differences between normal and chronic-and-pathological (cap) wounds?

Simply stated, intrinsic wound pathology and chronicity is a dynamical disorder of complex populations. The physics governing complex behaviors in complex systems is non-linear dynamics (nld). In addition to control, three aspects of NLD are especially important to wound pathology. (1) Population logistics. Healthy healing is a sequence of one-shot self-completing linear events: primary injury & thrombosis –then– acute inflammation –then– wound module. Pathology creates abnormal population dependencies (nutrition, starvation, predation, cultivation) and a new population, chronic inflammation. Non-linear perpetual complexity arises in the logistics of injury & thrombosis –vs– acute inflammation –vs– wound module –vs– chronic inflammation –vs– injury & thrombosis. (2) Cellular automata & self-organization. The “cellular” agents of the wound module (real biological cells in this case) have a small set of deterministic rules of interaction with each other. When allowed to function properly, stromal rebuilding is automatic and correct. Under pathological conditions, self-organization, i.e. wound healing is disrupted. (3) Chaos & N-body dynamics. The net effect is that the wound, a set of several interacting cell populations, has 3 attractors (basins, dynamically stable states or behaviors): convergence (healing), divergence (ulcerating), and self-sustained chaotic orbits (chronicity).

Basic methods to demonstrate non-linear dynamics: left, the logistical map of competing populations; middle, diffusion-limited-aggregation, an example of self-organizing automata; right, attractors and chaos in the Mandelbrot set of complex-plane iteration. While seemingly abstract, these structures are directly correlated with wound events.

53